W#08: Logistic Regression, Classification Problems, Prediction

Jan Lorenz

Logistic regression

Logistic regression

• Logistic regression is a GLM used to model a binary categorical outcome using numerical and categorical predictors.
• The distribution is the Bernoulli distribution with parameter \(p\) (success probability).
• As link function connecting \(\eta_i\) to \(p_i\) we use the logit function.

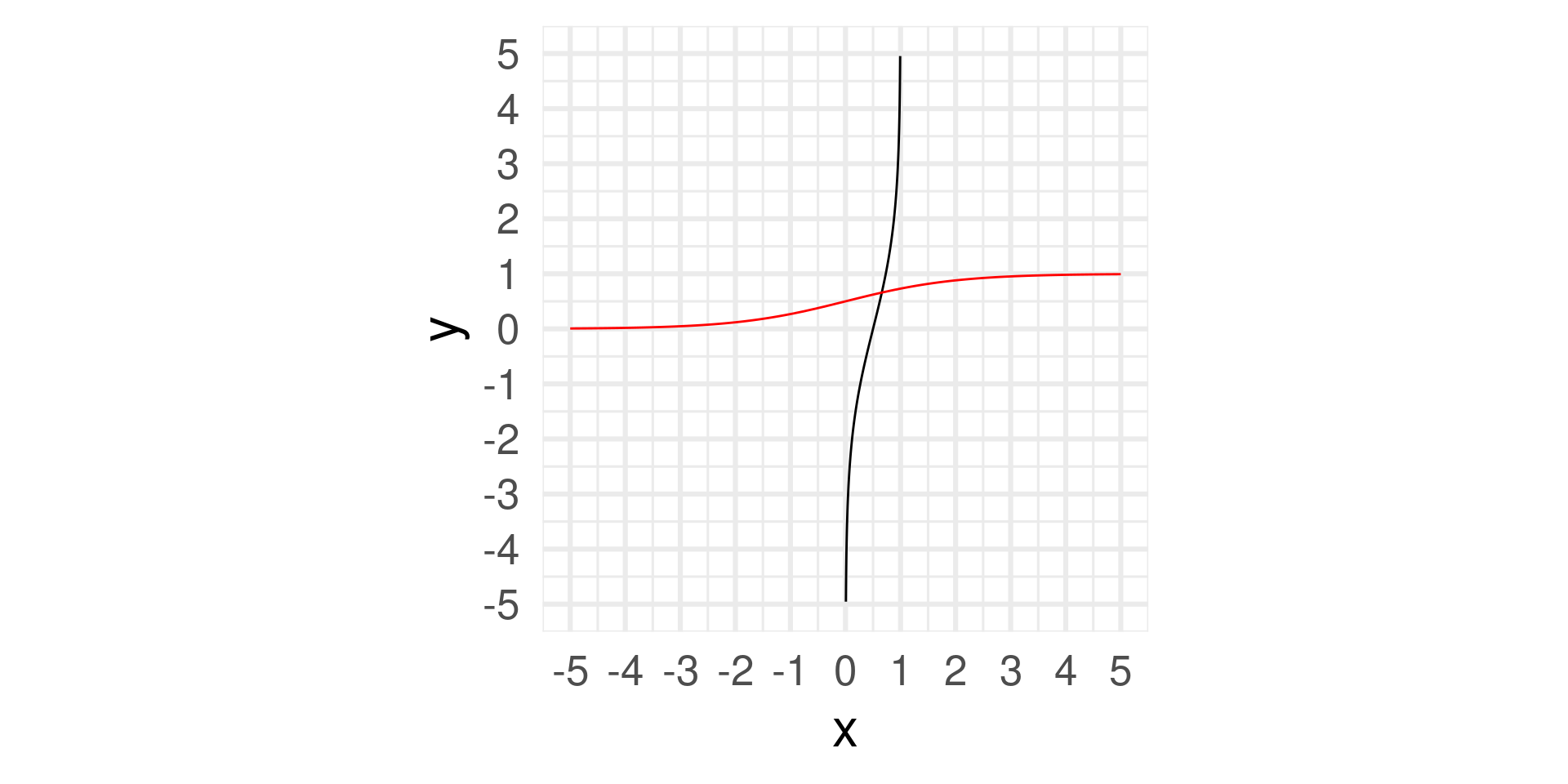
• Logit function: \(\text{logit}: [0,1] \to \mathbb{R}\)

\[\text{logit}(p) = \log\left(\frac{p}{1-p}\right)\]

• \(\frac{p}{1-p}\) is called the odds of a success which happens with probability \(p\).
  Example: Roll a six with a die has \(p=1/6\). Thus, the odds are \(\frac{1/6}{5/6} = 1/5\). Sometimes written as 1:5. “The odds of success are one to five.”

Properties of the logit

• Logit takes values between 0 and 1 and returns values between \(-\infty\) and \(\infty\)
• The inverse of the logit function if the logistic function (mapping values from \(-\infty\) and \(\infty\) to values between 0 and 1): \[\text{logit}^{-1}(x) = \text{logistic}(x) = \frac{e^x}{1+e^x} = \frac{1}{1+e^{-x}}\]
• Logit can be interpreted as the log odds of a success – more on this later.

• The logistic function is the solution of the differential equation \(\frac{d}{dx}f(x) = f(x)(1-f(x))\) which also appears in the SI-model of epidemics (and other models of exponential growth with saturation).
• Good exercises to check your math skills:
  1. Show that \(\text{logit}^{-1}(x) = \text{logistic}(x)\) or the other way round.
  2. Transform \(\frac{e^x}{1+e^x}\) into \(\frac{1}{1+e^{-x}}\).
  3. Check that \(\text{logistic}(x)\) is a solution to \(\frac{d}{dx}f(x) = f(x)(1-f(x))\).
• You can request hints from me when you get stuck.

Logit and logistic function

ggplot() + 
 geom_function(fun = function(x) log(x/(1-x)), xlim=c(0.001,0.999), n = 500) + 
 geom_function(fun = function(x) 1/(1 + exp(-x)), color = "red") +
 scale_x_continuous(breaks = seq(-5,5,1), limits = c(-5,5)) +
 scale_y_continuous(breaks = seq(-5,5,1), limits = c(-5,5)) +
 coord_fixed() + theme_minimal(base_size = 24) + labs(x = "x")

The logistic regression model

• Based on the three GLM criteria we have
  • \(y_i \sim \text{Bernoulli}(p_i)\)
  • \(\eta_i = \beta_0+\beta_1 x_{1,i} + \cdots + \beta_n x_{n,i}\)
  • \(\text{logit}(p_i) = \eta_i\)

• From which we get

\[p_i = \frac{e^{\beta_0+\beta_1 x_{1,i} + \cdots + \beta_k x_{k,i}}}{1 + e^{\beta_0+\beta_1 x_{1,i} + \cdots + \beta_k x_{k,i}}}\]

Modeling spam

With tidymodels we fit a GLM in the same way as a linear model except we

• specify the model with logistic_reg()
• use "glm" instead of "lm" as the engine
• define family = "binomial" for the link function to be used in the model

spam_fit <- logistic_reg() |>
  set_engine("glm") |>
  fit(spam ~ num_char, data = email, family = "binomial")
tidy(spam_fit)

# A tibble: 2 × 5
  term        estimate std.error statistic   p.value
  <chr>          <dbl>     <dbl>     <dbl>     <dbl>
1 (Intercept)  -1.80     0.0716     -25.1  2.04e-139
2 num_char     -0.0621   0.00801     -7.75 9.50e- 15

• The family is binomial because the Bernoulli distribution is a special case of the binomial distribution \(\text{Binomial}(n,p)\) with \(n=1\).
• The binomial distribution specifies the probability to have \(k\) successes in \(n\) Bernoulli trials with the same success probability \(p\).

Spam model

# A tibble: 2 × 5
  term        estimate std.error statistic   p.value
  <chr>          <dbl>     <dbl>     <dbl>     <dbl>
1 (Intercept)  -1.80     0.0716     -25.1  2.04e-139
2 num_char     -0.0621   0.00801     -7.75 9.50e- 15

Model: \[\log\left(\frac{p}{1-p}\right) = -1.80-0.0621\cdot \text{num_char}\]

Predicted probability: Examples

We can compute the predicted probability that an email with 2000 character is spam as follows:

\[\log\left(\frac{p}{1-p}\right) = -1.80-0.0621\cdot 2 = -1.9242\]

(Note: num_char is in thousands.)

\[\frac{p}{1-p} = e^{-1.9242} = 0.15 \Rightarrow p = 0.15 \cdot (1 - p)\]

\[p = 0.15 - 0.15\cdot p \Rightarrow 1.15\cdot p = 0.15\]

\[p = 0.15 / 1.15 = 0.13\]

Predicted probability

logistic <- function(t) 1/(1+exp(-t))
preds <- tibble(x=c(2,15,40), y = logistic(-1.80-0.0621*x))
email |> ggplot(aes(x = num_char, y = as.numeric(spam)-1)) + 
 geom_point(alpha = 0.2) + 
 geom_function(fun = function(x) logistic(-1.80-0.0621*x),color="red") +
 geom_point(data = preds, mapping = aes(x,y), color = "blue", size = 3)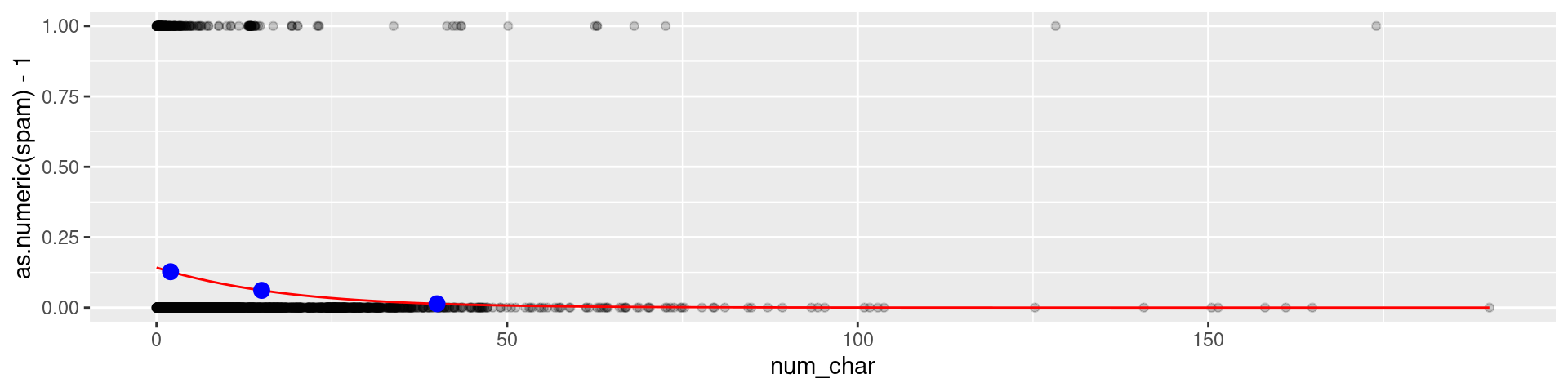

Spam probability 2,000 characters: 0.1273939
Spam probability 15,000 characters: 0.06114
Spam probability 40,000 characters: 0.0135999

Interpretation of coefficients

\[\log\left(\frac{p}{1-p}\right) = -1.80-0.0621\cdot \text{num_char}\]

What does an increase by thousand characters (num_char + 1) imply?

Let us assume the predicted probability of an email is \(p_0\). Then an increase of num_char by one implied that the log-odds become

\[\log\left(\frac{p_0}{1-p_0}\right) - 0.0621 = \log\left(\frac{p_0}{1-p_0}\right) - \log(e^{0.0621})\]

\[ = \log\left(\frac{p_0}{1-p_0}\right) + \log(\frac{1}{e^{0.0621}}) = \log\left(\frac{p_0}{1-p_0} \frac{1}{e^{0.0621}}\right) = \log\left(\frac{p_0}{1-p_0} 0.94\right)\]

That means the odds of being spam decrease by 6%.

Penguins example

library(palmerpenguins)
sex_fit <- logistic_reg() |>
  set_engine("glm") |>
  fit(sex ~ body_mass_g, data = na.omit(penguins), family = "binomial")
tidy(sex_fit)

# A tibble: 2 × 5
  term        estimate std.error statistic  p.value
  <chr>          <dbl>     <dbl>     <dbl>    <dbl>
1 (Intercept) -5.16     0.724        -7.13 1.03e-12
2 body_mass_g  0.00124  0.000173      7.18 7.10e-13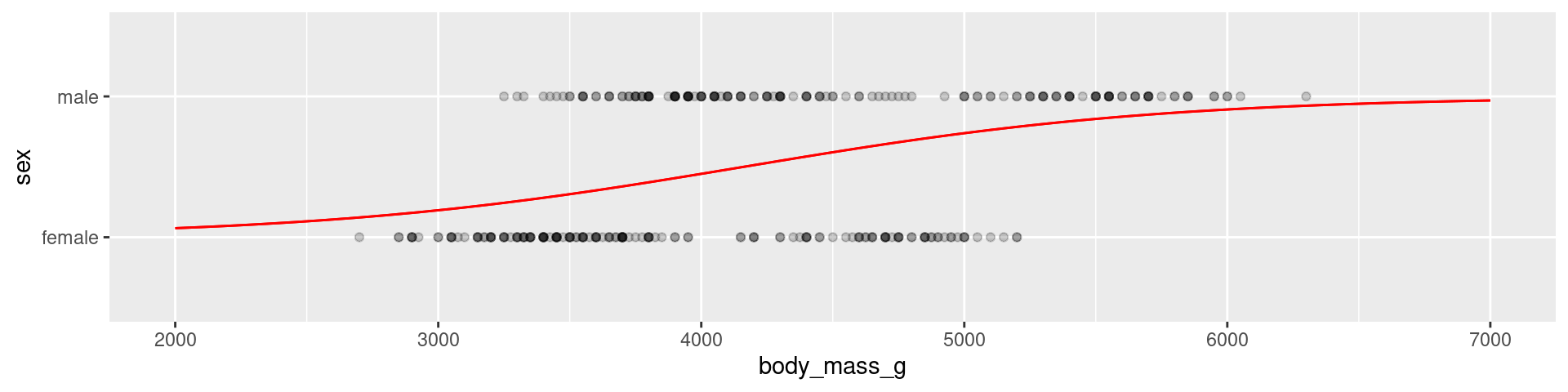

na.omit(penguins) |> ggplot(aes(x = body_mass_g, y = sex)) + 
 geom_point(alpha = 0.2) + 
 geom_function(fun = function(x) logistic(-5.16+0.00124*x) + 1,color="red") +
 xlim(c(2000,7000))

Summarizing the Idea of Logistic Regression

• We want to explain/predict a binary response variable.
• We want to use the concept of linear models.
• To that end we first interprete each outcome as the outcome of a probabilisitic event happening with probability \(p_i\). That way we transform the problem from modeling a binary outcome to a numerical outcome.
• However, probabilities are bounded between 0 and 1.
• We use the logit function to map probabilities to the real line. That means we predict the log-odds of the probability.
• We model the log-odds with a linear model.

Sensitivity and specificity

False positive and negative

	Email labelled spam	Email labelled not spam
Email is spam	True positive	False negative (Type 2 error)
Email is not spam	False positive (Type 1 error)	True negative

Confusion matrix

More general: Confusion matrix of statistical classification:

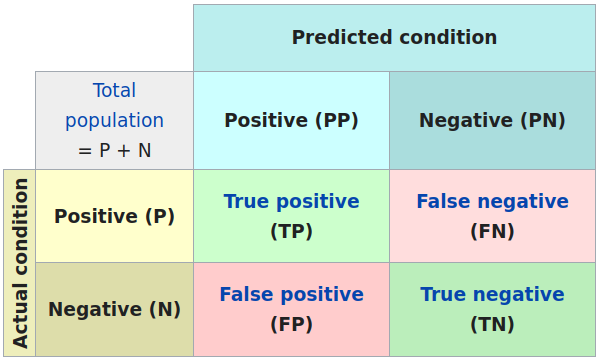
Sensitivity and specificity

Sensitivity is the true positive rate: TP / (TP + FN)
Specificity is the true negative rate: TN / (TN + FP)

For spam a positive case is an email labelled as spam:

Sensitivity: Fraction of emails labelled as spam among all emails which are spam.
Low sensitivity \(\to\) More false negatives \(\to\) More spam in you inbox!

Specificity: Fraction of emails labelled as not spam among all emails which are not spam.
Low specificity \(\to\) More false positives \(\to\) More relevant emails in spam folder!

If you were designing a spam filter, would you want sensitivity and specificity to be high or low? What are the trade-offs associated with each decision?

COVID-19 tests

A COVID-19 test is called positive when it indicates the presence of the virus.

What is the sensitivity of a test?

Probability the test is positive when the tested person has COVID-19. (The true positive rate.)

What is the specificity of a test?

Probability the test is negative when the tested person does not have COVID-19. (The true negative rate.)

Often the sensitivity is around 90% and the specificity is around 99%. What does that mean?

• When you do not have COVID the test is more likely to be correct, than when you do have COVID. However, specificity and sensitivity do not tell something about the probability to have COVID when the test is positive, or to not have COVID when the test is negative.

Another view

Prediction

Prediction vs. Explanation

Explanation and Prediction are different Modelling Mindsets¹.

• With an Explanatory Mindset we want to understand the relationship between the predictors and the outcome.
  • We interpret coefficients
  • We ask what variance can be explained by a linear model or a PCA
• With a Predictive Mindset we want to predict the outcome for new observations.
  • We use the model to predict the outcome for new observations
  • We ask how well we can predict the outcome for new observations
  • We may ignore why the model works

Important: The mindsets are very different but they may use the same models!

1. From Molnar, C. (2022). Modeling mindsets: The many cultures of learning from data. Christoph Molnar c/o Mucbook Clubhouse.

Prediction Example: Building a spam filter

• Data: Set of emails and we know
  • if each email is spam or not
  • several other features
• Use logistic regression to predict the probability that an incoming email is spam
• Use model selection to pick the model with the best predictive performance

• Building a model to predict the probability that an email is spam is only half of the battle! We also need a decision rule about which emails get flagged as spam (e.g. what probability should we use as out cutoff?)

• A simple approach: choose a single threshold probability and any email that exceeds that probability is flagged as spam

Emails: Use all predictors

logistic_reg() |>
  set_engine("glm") |>
  fit(spam ~ ., data = email, family = "binomial") |>
  tidy() |> print(n = 22)

Warning: glm.fit: fitted probabilities numerically 0 or 1 occurred

# A tibble: 22 × 5
   term         estimate std.error statistic  p.value
   <chr>           <dbl>     <dbl>     <dbl>    <dbl>
 1 (Intercept)  -9.09e+1   9.80e+3  -0.00928 9.93e- 1
 2 to_multiple1 -2.68e+0   3.27e-1  -8.21    2.25e-16
 3 from1        -2.19e+1   9.80e+3  -0.00224 9.98e- 1
 4 cc            1.88e-2   2.20e-2   0.855   3.93e- 1
 5 sent_email1  -2.07e+1   3.87e+2  -0.0536  9.57e- 1
 6 time          8.48e-8   2.85e-8   2.98    2.92e- 3
 7 image        -1.78e+0   5.95e-1  -3.00    2.73e- 3
 8 attach        7.35e-1   1.44e-1   5.09    3.61e- 7
 9 dollar       -6.85e-2   2.64e-2  -2.59    9.64e- 3
10 winneryes     2.07e+0   3.65e-1   5.67    1.41e- 8
11 inherit       3.15e-1   1.56e-1   2.02    4.32e- 2
12 viagra        2.84e+0   2.22e+3   0.00128 9.99e- 1
13 password     -8.54e-1   2.97e-1  -2.88    4.03e- 3
14 num_char      5.06e-2   2.38e-2   2.13    3.35e- 2
15 line_breaks  -5.49e-3   1.35e-3  -4.06    4.91e- 5
16 format1      -6.14e-1   1.49e-1  -4.14    3.53e- 5
17 re_subj1     -1.64e+0   3.86e-1  -4.25    2.16e- 5
18 exclaim_subj  1.42e-1   2.43e-1   0.585   5.58e- 1
19 urgent_subj1  3.88e+0   1.32e+0   2.95    3.18e- 3
20 exclaim_mess  1.08e-2   1.81e-3   5.98    2.23e- 9
21 numbersmall  -1.19e+0   1.54e-1  -7.74    9.62e-15
22 numberbig    -2.95e-1   2.20e-1  -1.34    1.79e- 1

We treat the warning later.

The prediction task

• The mechanics of prediction is easy:
  • Plug in values of predictors to the model equation
  • Calculate the predicted value of the response variable, \(\hat{y}\)

• Getting it right is harder
  • There is no guarantee the model estimates you have are correct
  • Or that your model will perform as well with new data as it did with your sample data

Balance Over- and Underfitting

In a one predictor model we can show both visually:

This is simulated data.

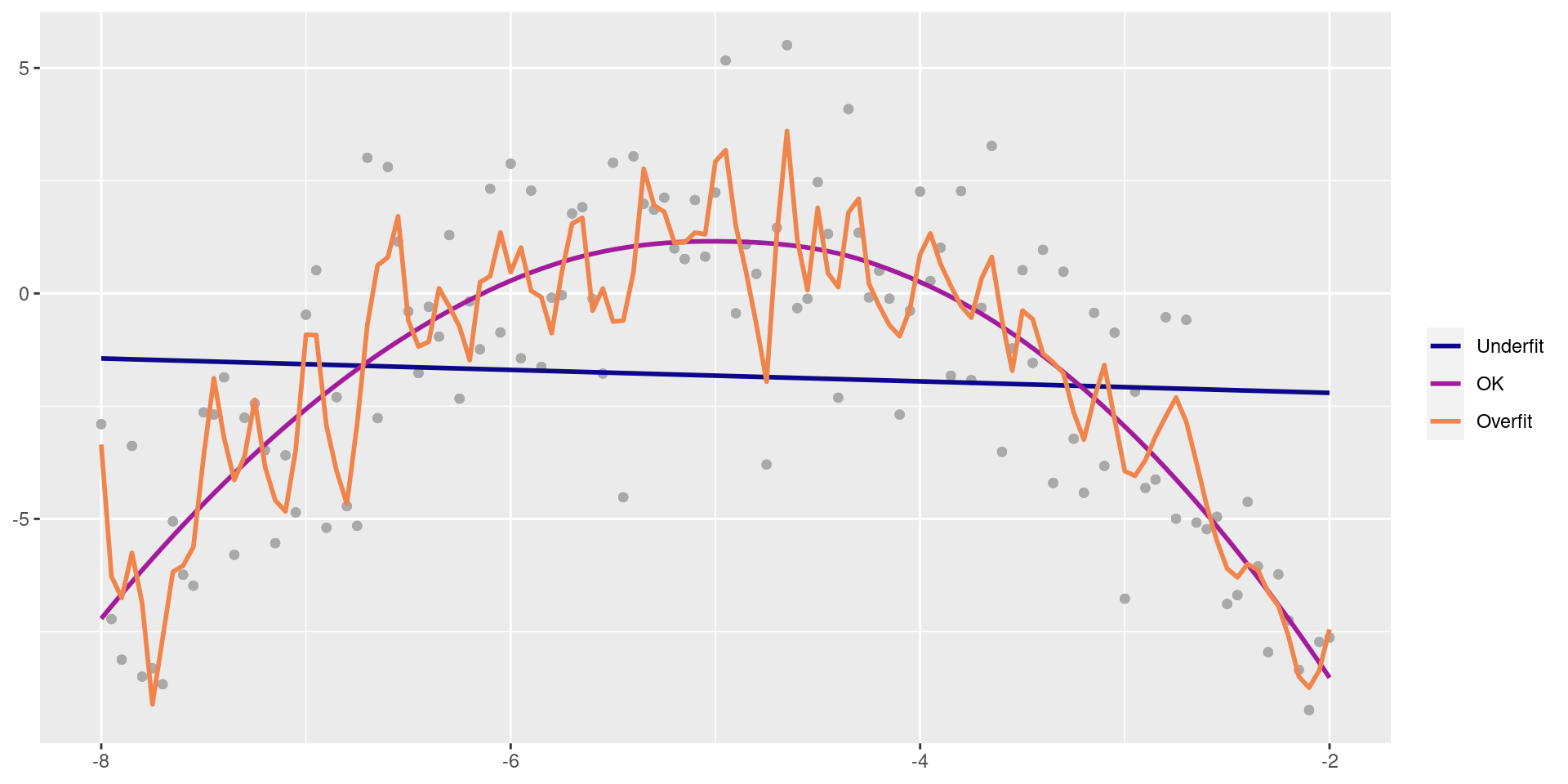
Spending our data

Problem:

• There are several steps to create a useful prediction model: parameter estimation, model selection, performance assessment, etc.
• Doing all of this on the entire data we have available can lead to overfitting.

Solution: We subsets our data for different tasks, as opposed to allocating all data to parameter estimation (as we have done so far).

Splitting Data

Splitting data

• Training set:
  • Sandbox for model building
  • Spend most of your time using the training set to develop the model
  • Majority of the data (usually 80%)
• Testing set:
  • Held in reserve to determine efficacy of one or two chosen models
  • Critical to look at it once, otherwise it becomes part of the modeling process
  • Remainder of the data (usually 20%)

Sidenote: Splitting data is very important for the predictive questions, because we want to know how well our model performs on new data. It is not relevant for explanatory questions where we want to interpret coefficients and infer about the underlying population.

Performing the split

# Fix random numbers by setting the seed 
# Enables analysis to be reproducible when random numbers are used 
set.seed(1116)

# Put 80% of the data into the training set 
email_split <- initial_split(email, prop = 0.80)

# Create data frames for the two sets:
train_data <- training(email_split)
test_data  <- testing(email_split)

A note on the seed: The seed is an arbitrary number that is used to initialize a pseudorandom number generator. The same seed will always result in the same sequence of pseudorandom numbers. This is useful for reproducibility.

Peek at the split

glimpse(train_data)

Rows: 3,136
Columns: 21
$ spam         <fct> 0, 1, 0, 1, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, …
$ to_multiple  <fct> 0, 0, 0, 0, 1, 1, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, …
$ from         <fct> 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, …
$ cc           <int> 2, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 35, 0, 0, 0, 0, 0,…
$ sent_email   <fct> 1, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, …
$ time         <dttm> 2012-01-25 23:46:55, 2012-01-03 06:28:28, 2012-02-04 17:…
$ image        <dbl> 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, …
$ attach       <dbl> 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, …
$ dollar       <dbl> 10, 0, 0, 0, 0, 0, 13, 0, 0, 0, 2, 0, 0, 0, 14, 0, 0, 0, …
$ winner       <fct> no, no, no, no, no, no, no, yes, no, no, no, no, no, no, …
$ inherit      <dbl> 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, …
$ viagra       <dbl> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, …
$ password     <dbl> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 3, 0, 0, …
$ num_char     <dbl> 23.308, 1.162, 4.732, 42.238, 1.228, 25.599, 16.764, 10.7…
$ line_breaks  <int> 477, 2, 127, 712, 30, 674, 367, 226, 98, 671, 46, 192, 67…
$ format       <fct> 1, 0, 1, 1, 0, 1, 1, 1, 1, 1, 0, 1, 0, 0, 1, 1, 1, 1, 1, …
$ re_subj      <fct> 1, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 1, 0, 0, 0, 1, …
$ exclaim_subj <dbl> 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 1, …
$ urgent_subj  <fct> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, …
$ exclaim_mess <dbl> 12, 0, 2, 2, 2, 31, 2, 0, 0, 1, 0, 1, 2, 0, 2, 0, 11, 1, …
$ number       <fct> small, none, big, big, small, small, small, small, small,…

glimpse(test_data)

Rows: 785
Columns: 21
$ spam         <fct> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, …
$ to_multiple  <fct> 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 1, 0, 0, 0, 0, 0, …
$ from         <fct> 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, …
$ cc           <int> 0, 1, 0, 1, 4, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 3, 0, …
$ sent_email   <fct> 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, …
$ time         <dttm> 2012-01-01 18:55:06, 2012-01-01 20:38:32, 2012-01-02 06:…
$ image        <dbl> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, …
$ attach       <dbl> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 1, 0, 0, …
$ dollar       <dbl> 0, 0, 5, 0, 0, 0, 0, 5, 4, 0, 0, 0, 21, 0, 0, 2, 9, 0, 0,…
$ winner       <fct> no, no, no, no, no, no, no, no, no, no, no, no, no, no, n…
$ inherit      <dbl> 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, …
$ viagra       <dbl> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, …
$ password     <dbl> 0, 0, 1, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 2, …
$ num_char     <dbl> 4.837, 15.075, 18.037, 45.842, 11.438, 1.482, 14.431, 0.9…
$ line_breaks  <int> 193, 354, 345, 881, 125, 24, 296, 13, 192, 14, 32, 30, 55…
$ format       <fct> 1, 1, 1, 1, 0, 1, 1, 0, 1, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, …
$ re_subj      <fct> 0, 1, 0, 1, 1, 0, 0, 0, 0, 0, 1, 0, 0, 0, 1, 0, 0, 1, 0, …
$ exclaim_subj <dbl> 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, …
$ urgent_subj  <fct> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, …
$ exclaim_mess <dbl> 1, 10, 20, 5, 2, 0, 0, 0, 6, 0, 0, 1, 3, 0, 4, 0, 1, 0, 1…
$ number       <fct> big, small, small, big, small, none, small, small, small,…

Workflow of Predictive Modeling

Fit a model to the training dataset

email_fit <- logistic_reg() |>
  set_engine("glm") |>
  fit(spam ~ ., data = train_data, family = "binomial")

Warning: glm.fit: fitted probabilities numerically 0 or 1 occurred

We get a warning and should explore the reasons for 0 or 1 probability.

• A deeper looking into the predicted probabilities (not shown here) shows that 4 cases are predicted to be spam with 100% probability, as well as 864 cases are predicted to be not spam with 100% probability.
• Note: The dplyr function near was used to assess if predicted probabilities were one.
• This is usually undesirable. Hence the warning.

Look at categorical predictors

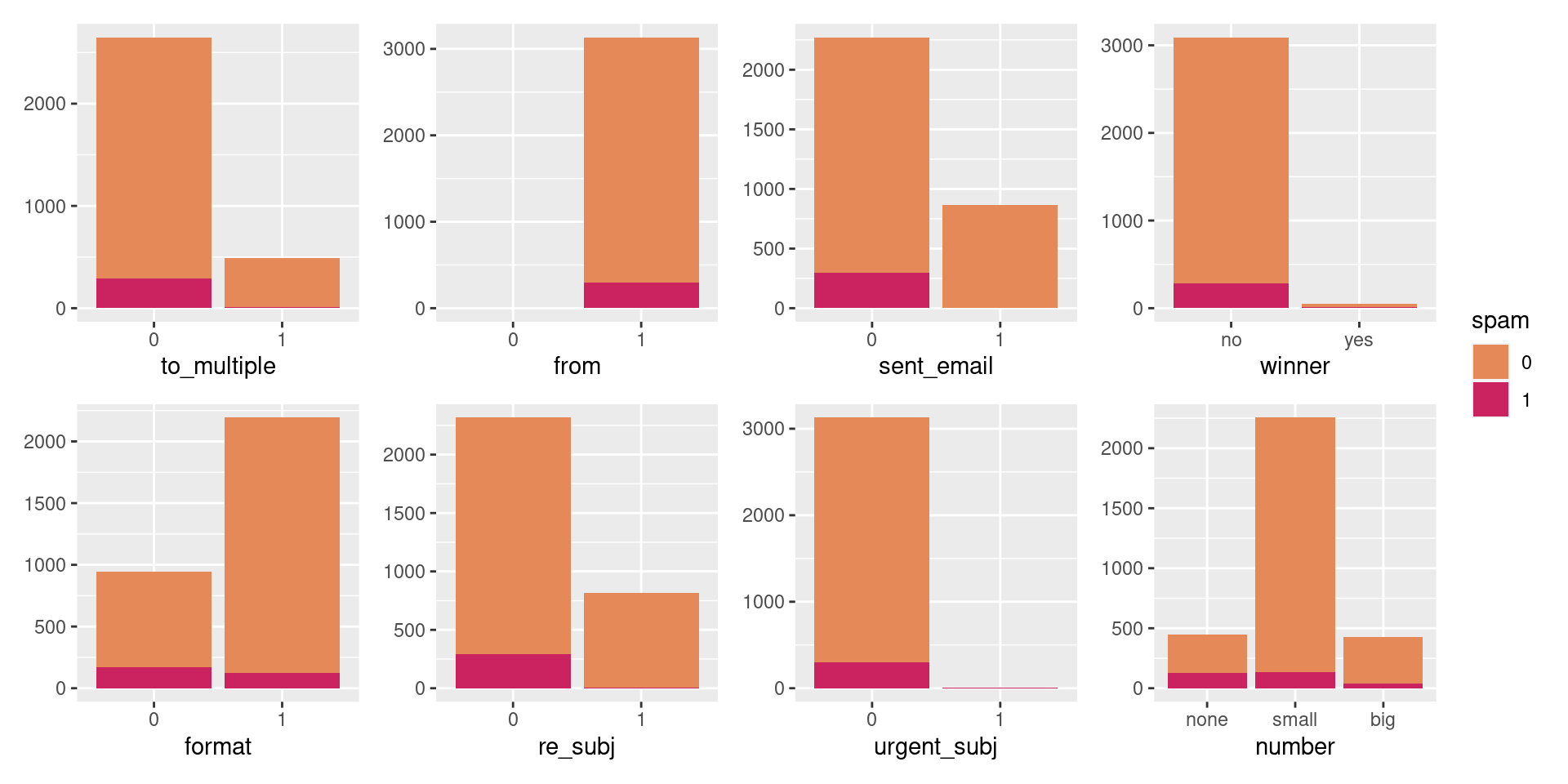
Closer look at from and sent_email.

Counting cases

from: Whether the message was listed as from anyone (this is usually set by default for regular outgoing email).

train_data |> count(spam, from)

# A tibble: 3 × 3
  spam  from      n
  <fct> <fct> <int>
1 0     1      2837
2 1     0         3
3 1     1       296

No non-spam mails without from.

sent_mail: Indicator for whether the sender had been sent an email from the receiver in the last 30 days.

train_data |> count(spam, sent_email)

# A tibble: 3 × 3
  spam  sent_email     n
  <fct> <fct>      <int>
1 0     0           1972
2 0     1            865
3 1     0            299

No spam mails with sent_email.

• There is incomplete separation in the data for those variables.
• That mean we have a sure prediction probabilities (0 or 1). (That is the warning. Also, these variables have the highest coefficients.)
• This is not what we assume about reality. Maybe our sample is too small to see it.
• Therefore we exclude these variables.

Look at numerical variables

train_data |>
 group_by(spam) |>
 select(where(is.numeric)) |> 
 pivot_longer(-spam) |> 
 group_by(name, spam) |> 
 summarize(mean = mean(value), sd = sd(value)) |> 
 print(n = 22)

# A tibble: 22 × 4
# Groups:   name [11]
   name         spam       mean       sd
   <chr>        <fct>     <dbl>    <dbl>
 1 attach       0       0.124     0.775 
 2 attach       1       0.227     0.620 
 3 cc           0       0.393     2.62  
 4 cc           1       0.388     3.25  
 5 dollar       0       1.56      5.33  
 6 dollar       1       0.779     3.01  
 7 exclaim_mess 0       6.68     50.2   
 8 exclaim_mess 1       8.75     88.4   
 9 exclaim_subj 0       0.0783    0.269 
10 exclaim_subj 1       0.0769    0.267 
11 image        0       0.0536    0.503 
12 image        1       0.00334   0.0578
13 inherit      0       0.0352    0.216 
14 inherit      1       0.0702    0.554 
15 line_breaks  0     247.      326.    
16 line_breaks  1     108.      321.    
17 num_char     0      11.4      14.9   
18 num_char     1       5.63     15.7   
19 password     0       0.112     0.938 
20 password     1       0.0201    0.182 
21 viagra       0       0         0     
22 viagra       1       0.0268    0.463 

viagra has no mentions in non-spam emails.

• We should exclude this variable for the same reason.

Fit a model to the training dataset

email_fit <- logistic_reg() |>
  set_engine("glm") |>
  fit(spam ~ . - from - sent_email - viagra, data = train_data, family = "binomial") 

Warning: glm.fit: fitted probabilities numerically 0 or 1 occurred

email_fit

parsnip model object


Call:  stats::glm(formula = spam ~ . - from - sent_email - viagra, family = stats::binomial, 
    data = data)

Coefficients:
 (Intercept)  to_multiple1            cc          time         image  
  -9.867e+01    -2.505e+00     1.944e-02     7.396e-08    -2.854e+00  
      attach        dollar     winneryes       inherit      password  
   5.070e-01    -6.440e-02     2.170e+00     4.499e-01    -7.065e-01  
    num_char   line_breaks       format1      re_subj1  exclaim_subj  
   5.870e-02    -5.420e-03    -9.017e-01    -2.995e+00     1.002e-01  
urgent_subj1  exclaim_mess   numbersmall     numberbig  
   3.572e+00     1.009e-02    -8.518e-01    -1.329e-01  

Degrees of Freedom: 3135 Total (i.e. Null);  3117 Residual
Null Deviance:      1974 
Residual Deviance: 1447     AIC: 1485

We still get a warning, but without very high coefficients.

A deeper analysis shows that now only two cases are predicted not spam with 100% probability.

Predict with the testing dataset

Predicting the raw values (log-odds)

predict(email_fit, test_data, type = "raw") |> head() # head prints the first values

        1         2         3         4         5         6 
-4.942500 -6.312226 -3.938487 -6.688992 -4.399541 -1.587700 

Predicting probabilities

predict(email_fit, test_data, type = "prob") |> head()

# A tibble: 6 × 2
  .pred_0 .pred_1
    <dbl>   <dbl>
1   0.993 0.00709
2   0.998 0.00181
3   0.981 0.0191 
4   0.999 0.00124
5   0.988 0.0121 
6   0.830 0.170  

Predicting spam (default)

predict(email_fit, test_data) # Would be type = "class"

# A tibble: 785 × 1
   .pred_class
   <fct>      
 1 0          
 2 0          
 3 0          
 4 0          
 5 0          
 6 0          
 7 0          
 8 0          
 9 0          
10 0          
# ℹ 775 more rows

Relate back to the model concept

email_pred <- 
 predict(email_fit, test_data, type = "prob") |>
 select(spam_prob = .pred_1) |> 
 mutate(spam_logodds = 
         predict(email_fit, test_data, type = "raw"), 
        spam_odds = exp(spam_logodds)) |> 
 bind_cols(predict(email_fit, test_data)) |> 
 # Append real data
 bind_cols(test_data |> select(spam)) 
email_pred

# A tibble: 785 × 5
   spam_prob spam_logodds spam_odds .pred_class spam 
       <dbl>        <dbl>     <dbl> <fct>       <fct>
 1   0.00709        -4.94   0.00714 0           0    
 2   0.00181        -6.31   0.00181 0           0    
 3   0.0191         -3.94   0.0195  0           0    
 4   0.00124        -6.69   0.00124 0           0    
 5   0.0121         -4.40   0.0123  0           0    
 6   0.170          -1.59   0.204   0           0    
 7   0.0410         -3.15   0.0427  0           0    
 8   0.139          -1.83   0.161   0           0    
 9   0.0617         -2.72   0.0657  0           0    
10   0.0983         -2.22   0.109   0           0    
# ℹ 775 more rows

• The raw predictions are the log-odds.
• From which we can compute the odds.
• From which the probability is computed. Here it is done by predict.
• The .pred_class prediction is when the probability > 0.5.
  • What does it mean for the odds and the log-odds?

Answers: odds > 1, log-odds > 0

Another look

email_pred |> arrange(desc(spam_prob)) |> print(n = 20)

# A tibble: 785 × 5
   spam_prob spam_logodds spam_odds .pred_class spam 
       <dbl>        <dbl>     <dbl> <fct>       <fct>
 1     0.903       2.23       9.29  1           1    
 2     0.833       1.60       4.98  1           0    
 3     0.825       1.55       4.71  1           1    
 4     0.733       1.01       2.75  1           1    
 5     0.683       0.766      2.15  1           1    
 6     0.626       0.517      1.68  1           1    
 7     0.614       0.464      1.59  1           0    
 8     0.597       0.392      1.48  1           1    
 9     0.538       0.153      1.17  1           1    
10     0.537       0.148      1.16  1           0    
11     0.510       0.0404     1.04  1           0    
12     0.491      -0.0345     0.966 0           0    
13     0.490      -0.0407     0.960 0           0    
14     0.489      -0.0453     0.956 0           1    
15     0.483      -0.0698     0.933 0           1    
16     0.473      -0.107      0.899 0           0    
17     0.463      -0.150      0.861 0           0    
18     0.457      -0.174      0.840 0           0    
19     0.447      -0.212      0.809 0           0    
20     0.447      -0.214      0.808 0           1    
# ℹ 765 more rows

We see false positives and false negatives.

Evaluate the performance

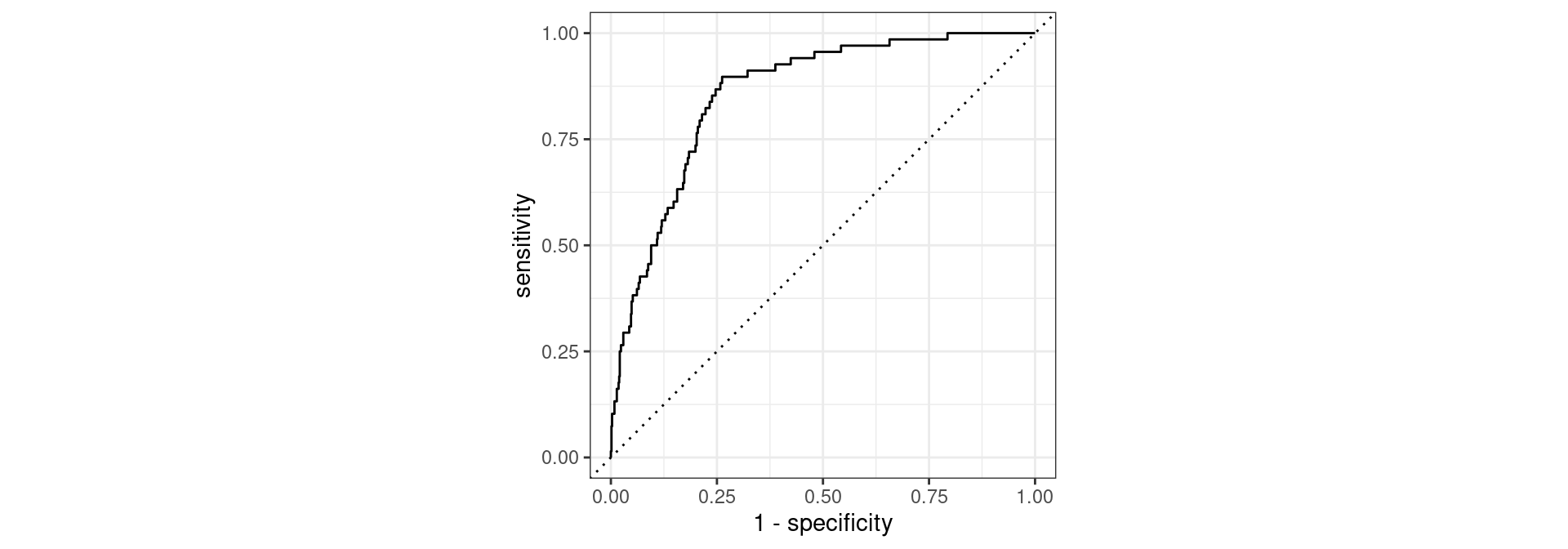
Receiver operating characteristic (ROC) curve¹ which plots true positive rate (sensitivity) vs. false positive rate (1 - specificity)

email_pred |> roc_curve(
    truth = spam, spam_prob,
    event_level = "second" # this adjusts the location above the diagonal
  ) |> autoplot()

1. Originally developed for operators of military radar receivers, hence the odd name.

Evaluate the performance

Find the area under the curve (AUC).

In calculus language:
\(\int_0^1 \text{TPR}(\text{FPR}) d\text{FPR}\)

Remember:

• TPR = True Positive Rate = sensitivity
• FPR = False Positive Rate = 1 - specificity
• specificity is the true negative rate.

email_pred |>
  roc_auc(
    truth = spam,
    spam_prob,
    event_level = "second" 
  )

# A tibble: 1 × 3
  .metric .estimator .estimate
  <chr>   <chr>          <dbl>
1 roc_auc binary         0.857

Feature engineering

Feature engineering

• We prefer simple models when possible, but parsimony does not mean sacrificing accuracy (or predictive performance) in the interest of simplicity
• Variables that go into the model and how they are represented are critical to the success of the model
• Feature engineering is getting creative with our predictors in an effort to make them more useful for our model (to increase its predictive performance)

Modeling workflow, revisited

• Create a recipe for feature engineering steps to be applied to the training data

  • The tidymodels way (similar to a pipeline in python’s scikit-learn).

• Fit the model to the training data after these steps have been applied

• Using the model estimates from the training data, predict outcomes for the test data

• Evaluate the performance of the model on the test data

Recipes

Initiate a recipe

email_rec <- recipe(
 spam ~ .,          # formula
 data = train_data  # data to use for cataloguing names and types of variables
)
summary(email_rec) |> print(n = 21)

# A tibble: 21 × 4
   variable     type      role      source  
   <chr>        <list>    <chr>     <chr>   
 1 to_multiple  <chr [3]> predictor original
 2 from         <chr [3]> predictor original
 3 cc           <chr [2]> predictor original
 4 sent_email   <chr [3]> predictor original
 5 time         <chr [1]> predictor original
 6 image        <chr [2]> predictor original
 7 attach       <chr [2]> predictor original
 8 dollar       <chr [2]> predictor original
 9 winner       <chr [3]> predictor original
10 inherit      <chr [2]> predictor original
11 viagra       <chr [2]> predictor original
12 password     <chr [2]> predictor original
13 num_char     <chr [2]> predictor original
14 line_breaks  <chr [2]> predictor original
15 format       <chr [3]> predictor original
16 re_subj      <chr [3]> predictor original
17 exclaim_subj <chr [2]> predictor original
18 urgent_subj  <chr [3]> predictor original
19 exclaim_mess <chr [2]> predictor original
20 number       <chr [3]> predictor original
21 spam         <chr [3]> outcome   original

The object email_rec only includes meta-data (columns names and types)!

Remove certain variables

email_rec |>
  step_rm(from, sent_email, viagra)

Feature engineer date

• The date-time may not be such an interesting predictor.
  • It could only bring in a general trend over time
• Often decomposing the date to the month or the day of the week (dow) is more interesting.
  • step_date can easily extract these

email_rec |>
 step_rm(from, sent_email, viagra) |> 
 step_date(time, features = c("dow", "month")) |>
 step_rm(time)

Create dummy variables

• Use helper functions like all_nominal or all_outcomes from tidymodels for column selection.

email_rec |>
 step_rm(from, sent_email, viagra) |> 
 step_date(time, features = c("dow", "month")) |>
 step_rm(time) |> 
 step_dummy(all_nominal(), -all_outcomes()) 

Remove zero variance variables

Variables that contain only a single value.

email_rec |>
 step_rm(from, sent_email, viagra) |> 
 step_date(time, features = c("dow", "month")) |>
 step_rm(time) |> 
 step_dummy(all_nominal(), -all_outcomes()) |> 
 step_zv(all_predictors())

Full recipe

email_rec <- recipe(
 spam ~ .,          # formula
 data = train_data  # data to use for cataloguing names and types of variables
) |>
 step_rm(from, sent_email, viagra) |> 
 step_date(time, features = c("dow", "month")) |>
 step_rm(time) |> 
 step_dummy(all_nominal(), -all_outcomes()) |> 
 step_zv(all_predictors())
print(email_rec)

── Recipe ──────────────────────────────────────────────────────────────────────

── Inputs 

Number of variables by role

outcome:    1
predictor: 20

── Operations 

• Variables removed: from, sent_email, viagra

• Date features from: time

• Variables removed: time

• Dummy variables from: all_nominal(), -all_outcomes()

• Zero variance filter on: all_predictors()

The object email_rec only includes meta-data of the data frame it shall work on (a formula, columns names and types)!

Building workflows

Define model

email_mod <- logistic_reg() |> 
  set_engine("glm")

email_mod

Logistic Regression Model Specification (classification)

Computational engine: glm 

Define workflow

Workflows bring together models and recipes so that they can be easily applied to both the training and test data.

email_wflow <- workflow() |> 
  add_model(email_mod) |> 
  add_recipe(email_rec)
email_wflow

══ Workflow ════════════════════════════════════════════════════════════════════
Preprocessor: Recipe
Model: logistic_reg()

── Preprocessor ────────────────────────────────────────────────────────────────
5 Recipe Steps

• step_rm()
• step_date()
• step_rm()
• step_dummy()
• step_zv()

── Model ───────────────────────────────────────────────────────────────────────
Logistic Regression Model Specification (classification)

Computational engine: glm 

Fit model to training data

email_fit <- email_wflow |> 
  fit(data = train_data)

tidy(email_fit) |> print(n = 27)

# A tibble: 27 × 5
   term            estimate std.error statistic  p.value
   <chr>              <dbl>     <dbl>     <dbl>    <dbl>
 1 (Intercept)     -0.651     0.254     -2.57   1.03e- 2
 2 cc               0.0214    0.0229     0.936  3.49e- 1
 3 image           -2.99      1.31      -2.28   2.28e- 2
 4 attach           0.512     0.116      4.41   1.03e- 5
 5 dollar          -0.0651    0.0307    -2.12   3.40e- 2
 6 inherit          0.440     0.205      2.15   3.14e- 2
 7 password        -0.723     0.302     -2.39   1.67e- 2
 8 num_char         0.0585    0.0240     2.43   1.50e- 2
 9 line_breaks     -0.00548   0.00139   -3.94   8.24e- 5
10 exclaim_subj     0.0998    0.268      0.373  7.09e- 1
11 exclaim_mess     0.0103    0.00198    5.20   2.02e- 7
12 to_multiple_X1  -2.56      0.339     -7.56   4.11e-14
13 winner_yes       2.24      0.430      5.21   1.90e- 7
14 format_X1       -0.953     0.157     -6.06   1.38e- 9
15 re_subj_X1      -3.00      0.444     -6.76   1.39e-11
16 urgent_subj_X1   3.69      1.15       3.20   1.37e- 3
17 number_small    -0.840     0.162     -5.20   1.98e- 7
18 number_big      -0.0915    0.244     -0.375  7.07e- 1
19 time_dow_Mon    -0.326     0.303     -1.08   2.82e- 1
20 time_dow_Tue     0.0813    0.275      0.296  7.67e- 1
21 time_dow_Wed    -0.260     0.275     -0.946  3.44e- 1
22 time_dow_Thu    -0.220     0.279     -0.788  4.31e- 1
23 time_dow_Fri    -0.0612    0.275     -0.223  8.24e- 1
24 time_dow_Sat     0.0646    0.292      0.221  8.25e- 1
25 time_month_Feb   0.760     0.178      4.26   2.03e- 5
26 time_month_Mar   0.506     0.178      2.85   4.40e- 3
27 time_month_Apr -12.0     394.        -0.0306 9.76e- 1

Make predictions for test data

email_pred <- predict(email_fit, test_data, type = "prob") |> 
  bind_cols(test_data) 

email_pred

# A tibble: 785 × 23
   .pred_0  .pred_1 spam  to_multiple from     cc sent_email time               
     <dbl>    <dbl> <fct> <fct>       <fct> <int> <fct>      <dttm>             
 1   0.993 0.00653  0     1           1         0 1          2012-01-01 18:55:06
 2   0.998 0.00169  0     0           1         1 1          2012-01-01 20:38:32
 3   0.987 0.0127   0     0           1         0 0          2012-01-02 06:42:16
 4   0.999 0.000825 0     0           1         1 0          2012-01-02 16:12:51
 5   0.991 0.00876  0     0           1         4 0          2012-01-02 17:45:36
 6   0.878 0.122    0     0           1         0 0          2012-01-02 22:55:03
 7   0.959 0.0414   0     0           1         0 0          2012-01-03 02:07:17
 8   0.852 0.148    0     0           1         0 0          2012-01-03 06:41:35
 9   0.938 0.0619   0     0           1         0 0          2012-01-03 17:02:35
10   0.896 0.104    0     0           1         0 0          2012-01-03 12:14:51
# ℹ 775 more rows
# ℹ 15 more variables: image <dbl>, attach <dbl>, dollar <dbl>, winner <fct>,
#   inherit <dbl>, viagra <dbl>, password <dbl>, num_char <dbl>,
#   line_breaks <int>, format <fct>, re_subj <fct>, exclaim_subj <dbl>,
#   urgent_subj <fct>, exclaim_mess <dbl>, number <fct>

Evaluate the performance

email_pred |>
  roc_curve(
    truth = spam,
    .pred_1,
    event_level = "second"
  ) |>
  autoplot()

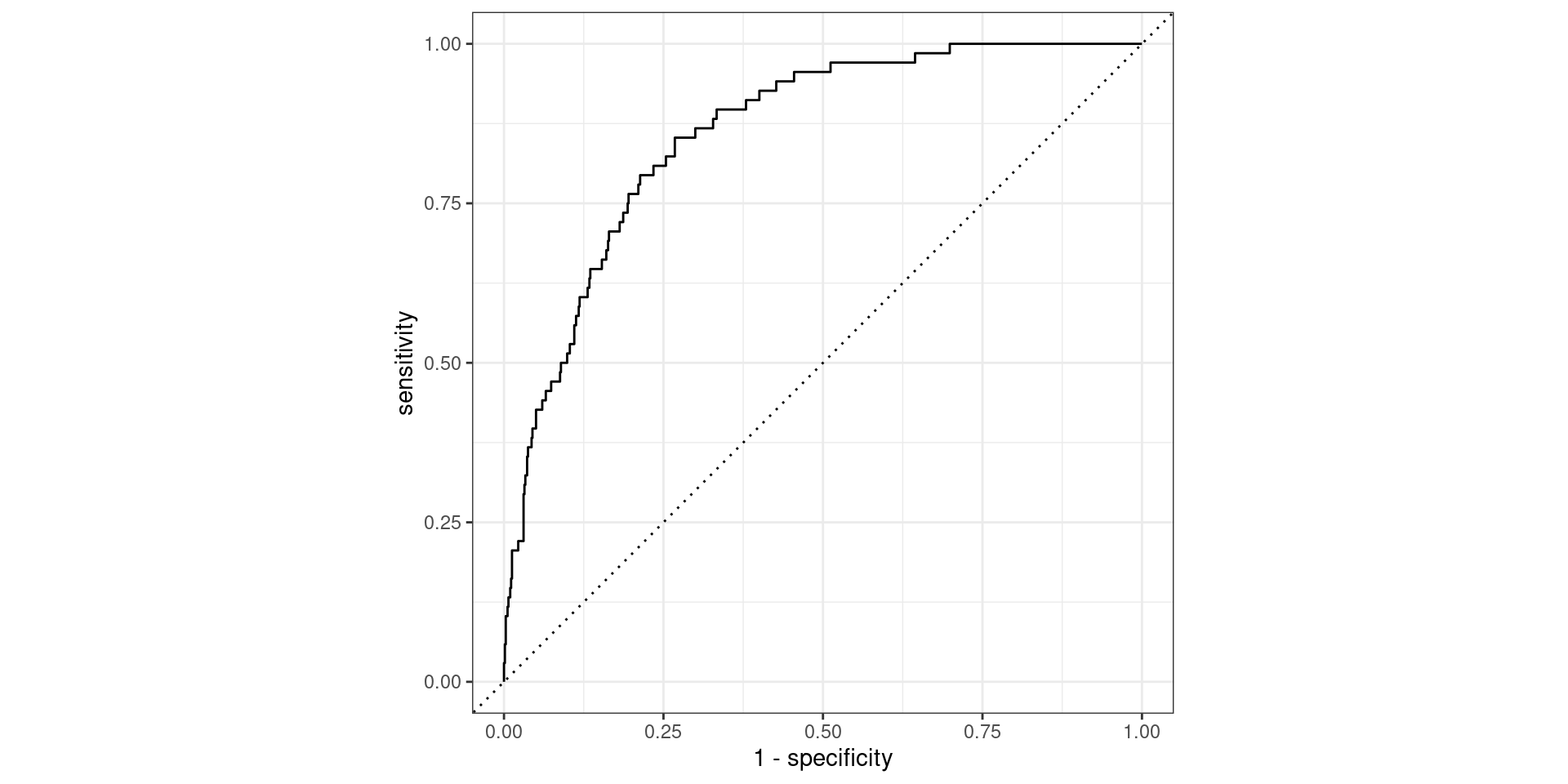
Evaluate the performance

email_pred |>
  roc_auc(
    truth = spam,
    .pred_1,
    event_level = "second"
  )

# A tibble: 1 × 3
  .metric .estimator .estimate
  <chr>   <chr>          <dbl>
1 roc_auc binary         0.860

This is better than our former model (without the feature engineering workflow), which had AUC = 0.857.

Making decisions

Cutoff probability: 0.5

Suppose we decide to label an email as spam if the model predicts the probability of spam to be more than 0.5. (That is the default.)

Confusion matrix:

cutoff_prob <- 0.5
email_pred |>
  mutate(
    spam      = if_else(spam == 1, "Email is spam", "Email is not spam"),
    spam_pred = if_else(.pred_1 > cutoff_prob, "Email labelled spam", "Email labelled not spam")
    ) |>
  count(spam_pred, spam) |>
  pivot_wider(names_from = spam_pred, values_from = n) |> 
  select(1,3,2) |> slice(c(2,1)) |> # reorder rows and cols to fit convention
  knitr::kable()

spam	Email labelled spam	Email labelled not spam
Email is spam	14	54
Email is not spam	10	707

Sensitivity: 14/(14+54) = 0.206
Specificity: 707/(707+10) = 0.986

Cutoff probability: 0.25

Suppose we decide to label an email as spam if the model predicts the probability of spam to be more than 0.25.

Confusion matrix:

spam	Email labelled spam	Email labelled not spam
Email is spam	32	36
Email is not spam	61	656

Sensitivity: 32/(32+36) = 0.471
Specificity: 656/(656 + 61) = 0.915

Cutoff probability: 0.75

Suppose we decide to label an email as spam if the model predicts the probability of spam to be more than 0.75.

Confusion matrix:

spam	Email labelled spam	Email labelled not spam
Email is spam	3	65
Email is not spam	1	716

Sensitivity: 3/(3+65) = 0.044
Specificity: 716/(716+1) = 0.999

Check our very first model

We make a new simple recipe and draw workflow and fitting re-using the same specified logisitc regression model email_mod.

simple_email_rec <- recipe(
 spam ~ num_char,          # formula
 data = train_data  # data to use for cataloguing names and types of variables
)
simple_email_pred <- 
 workflow() |> 
 add_model(email_mod) |> 
 add_recipe(simple_email_rec) |> 
 fit(data = train_data) |> 
 predict(test_data, type = "prob") |> 
 bind_cols(test_data |> select(spam,num_char,time)) 
simple_email_pred 

# A tibble: 785 × 5
   .pred_0 .pred_1 spam  num_char time               
     <dbl>   <dbl> <fct>    <dbl> <dttm>             
 1   0.889  0.111  0        4.84  2012-01-01 18:55:06
 2   0.936  0.0644 0       15.1   2012-01-01 20:38:32
 3   0.945  0.0547 0       18.0   2012-01-02 06:42:16
 4   0.989  0.0113 0       45.8   2012-01-02 16:12:51
 5   0.922  0.0784 0       11.4   2012-01-02 17:45:36
 6   0.868  0.132  0        1.48  2012-01-02 22:55:03
 7   0.933  0.0667 0       14.4   2012-01-03 02:07:17
 8   0.864  0.136  0        0.978 2012-01-03 06:41:35
 9   0.905  0.0953 0        7.79  2012-01-03 17:02:35
10   0.864  0.136  0        0.978 2012-01-03 12:14:51
# ℹ 775 more rows

Evaluate the performance

simple_email_pred |> roc_curve(
    truth = spam, 
    .pred_1,
    event_level = "second" # this adjusts the location above the diagonal
  ) |> autoplot()

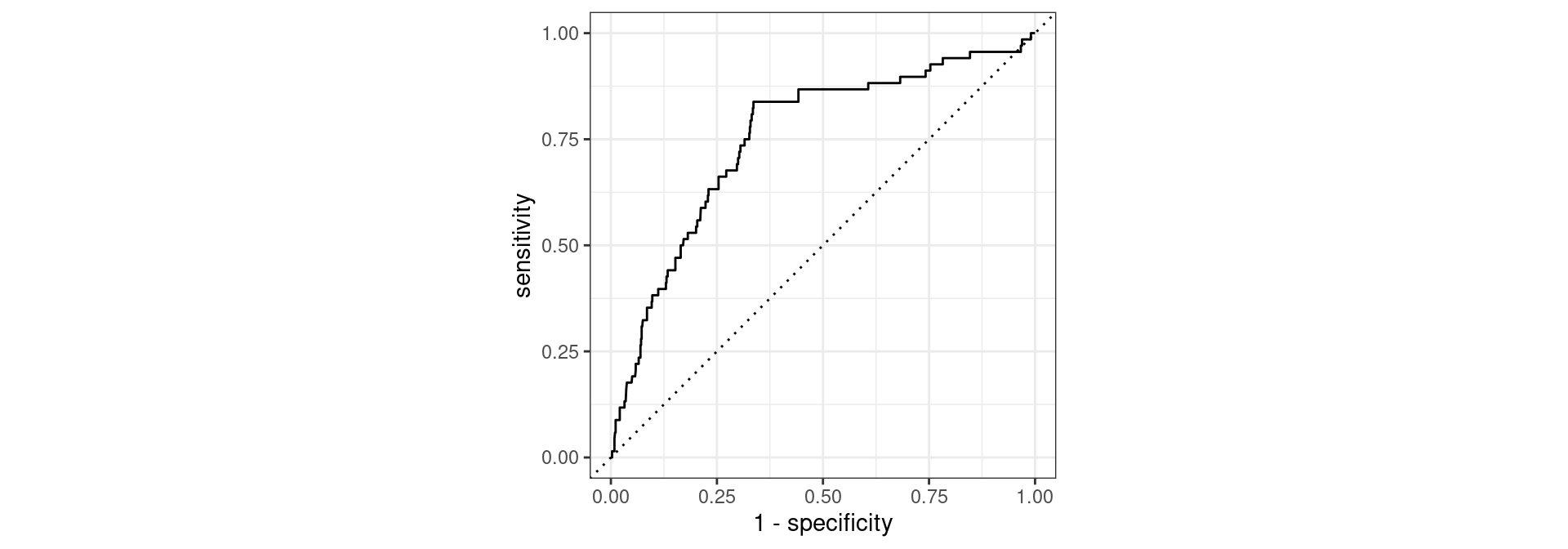
# A tibble: 1 × 3
  .metric .estimator .estimate
  <chr>   <chr>          <dbl>
1 roc_auc binary         0.753

Conclusion: It is not as good compared to AUC 0.86

Predict Penguins’ Sex

Following all the steps introduced before:

set.seed(1)
# Put 80% of the data into the training set 
peng_split <- initial_split(penguins, prop = 0.80)
# Create data frames for the two sets:
train_data_peng <- training(peng_split)
test_data_peng  <- testing(peng_split)

# Create a recipe for the model
peng_rec <- recipe(
 sex ~ .,
 data = train_data_peng 
) |> 
 step_naomit(all_predictors()) |> 
 step_dummy(all_nominal(), -all_outcomes()) |> 
 step_zv(all_predictors())

# Create a logistic regression model 
peng_mod <- logistic_reg() |> 
 set_engine("glm")

# Create a workflow
peng_wflow <- workflow() |> 
 add_model(peng_mod) |> 
 add_recipe(peng_rec)

# Fitting model to training data
peng_fit <- peng_wflow |> 
 fit(data = train_data_peng)

# Make predictions for test data
peng_pred <- peng_fit |> 
 predict(test_data_peng, type = "prob") |> 
 bind_cols(test_data_peng)

Penguins: Evaluate Performance

peng_pred |> roc_curve(
    truth = sex,  .pred_male, event_level = "second"
  ) |>  autoplot()

peng_pred |> roc_auc(
 truth = sex, .pred_male, event_level = "second")

# A tibble: 1 × 3
  .metric .estimator .estimate
  <chr>   <chr>          <dbl>
1 roc_auc binary         0.958

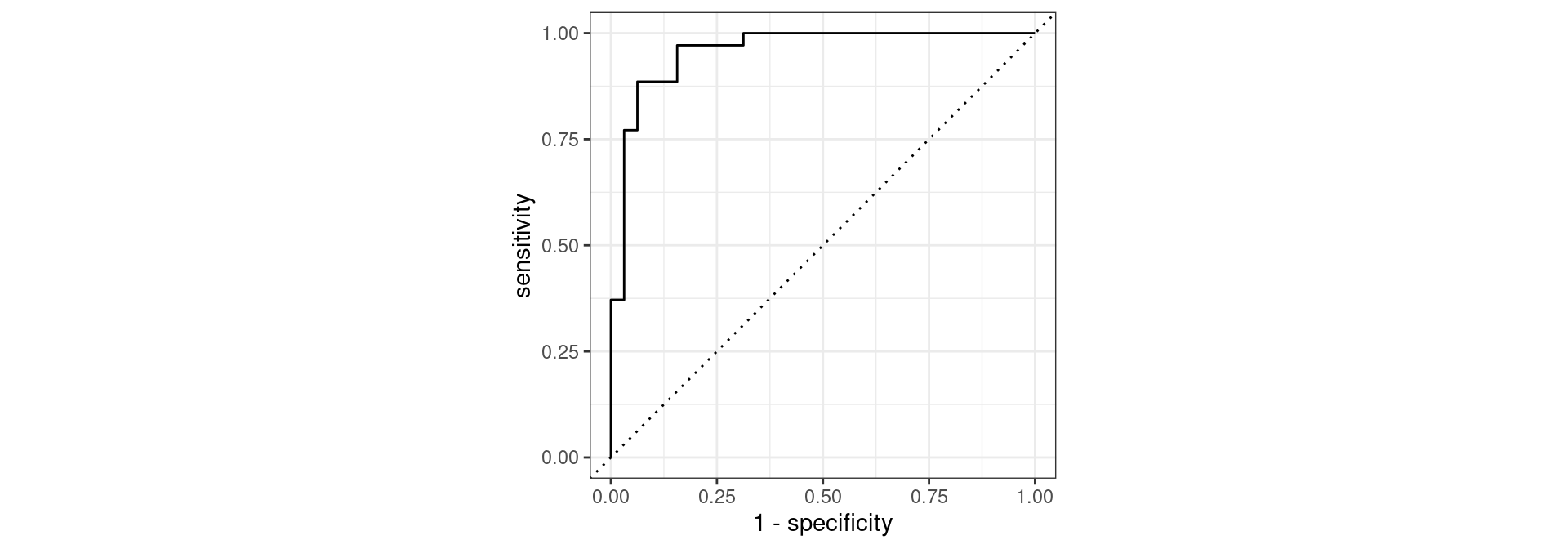
Penguins: Cutoff probability 0.5

Confusion matrix:

cutoff_prob <- 0.5
peng_pred |>
  mutate(
    sex      = if_else(sex == "male", "Penguin is male", "Penguin is female"),
    sex_pred = if_else(.pred_male > cutoff_prob, "Penguin labelled male", "Penguin labelled female")
    ) |>
  count(sex_pred, sex) |>
  pivot_wider(names_from = sex_pred, values_from = n) |> 
  select(1,3,2) |> slice(c(2,1)) |> # reorder rows and cols to fit convention
  knitr::kable()

sex	Penguin labelled male	Penguin labelled female
Penguin is male	31	4
Penguin is female	4	28

Sensitivity: 31/(31+4) = 0.886
Specificity: 28/(28+4) = 0.875

Penguins: Cutoff probability 0.25

Confusion matrix:

cutoff_prob <- 0.25
peng_pred |>
  mutate(
    sex      = if_else(sex == "male", "Penguin is male", "Penguin is female"),
    sex_pred = if_else(.pred_male > cutoff_prob, "Penguin labelled male", "Penguin labelled female")
    ) |>
  count(sex_pred, sex) |>
  pivot_wider(names_from = sex_pred, values_from = n) |> 
  select(1,3,2) |> slice(c(2,1)) |> # reorder rows and cols to fit convention
  knitr::kable()

sex	Penguin labelled male	Penguin labelled female
Penguin is male	34	1
Penguin is female	7	25

Sensitivity: 34/(34+1) = 0.971
Specificity: 25/(25+7) = 0.781

Penguins: Cutoff probability 0.75

Confusion matrix:

cutoff_prob <- 0.75
peng_pred |>
  mutate(
    sex      = if_else(sex == "male", "Penguin is male", "Penguin is female"),
    sex_pred = if_else(.pred_male > cutoff_prob, "Penguin labelled male", "Penguin labelled female")
    ) |>
  count(sex_pred, sex) |>
  pivot_wider(names_from = sex_pred, values_from = n) |> 
  select(1,3,2) |> slice(c(2,1)) |> # reorder rows and cols to fit convention
  knitr::kable()

sex	Penguin labelled male	Penguin labelled female
Penguin is male	29	6
Penguin is female	2	30

Sensitivity: 29/(29+6) = 0.829
Specificity: 30/(30+2) = 0.938