W#06: Epidemic Modeling, Calculus, Linear Model, Fitting a Linear Model
Epidemic Modeling
SIR model
- Assume a population of \(N\) individuals.
- Individuals can have different states, e.g.: Susceptible, Infectious, Recovered, …
- The population divides into compartments of these states which change over time, e.g.: \(S(t), I(t), R(t)\) number of susceptible, infectious, recovered individuals
Now we define dynamics like
where the numbers on the arrows represent transition probabilities.
Agent-based Simulation
Agent-based model: Individual agents are simulated and interact with each other.
Explore and analyze with computer simulations.
A tool: NetLogo https://ccl.northwestern.edu/netlogo/
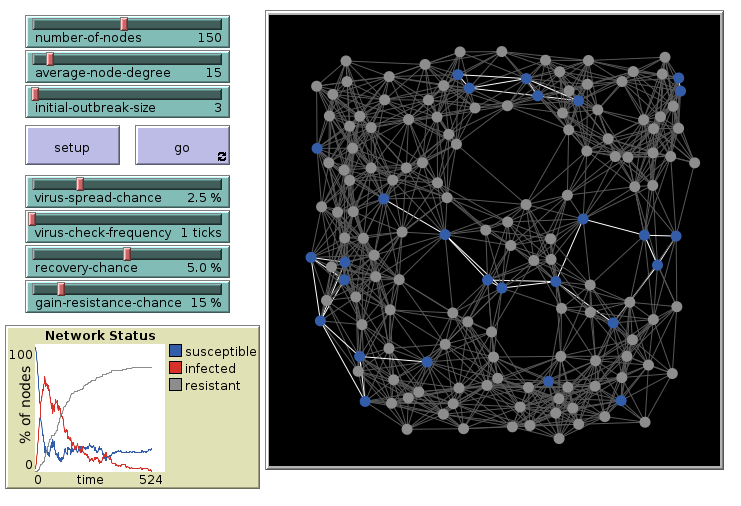
We look at the model “Virus on a Network” from the model library.
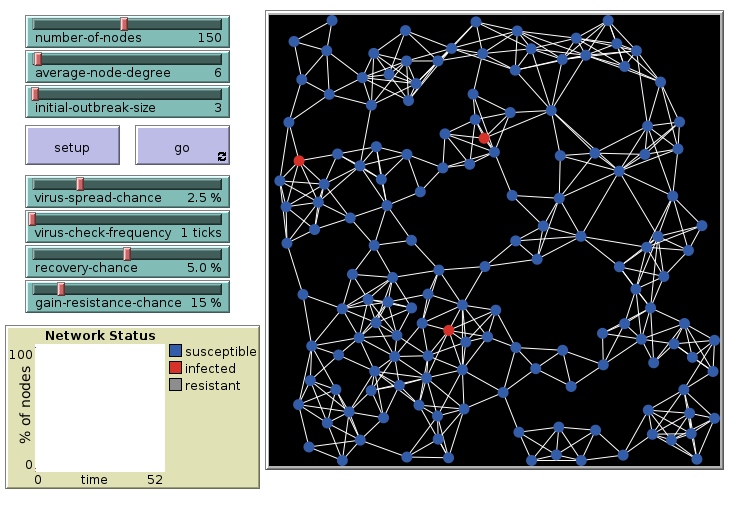
Virus on a Network: 6 links, initial
Agents connected in a network with on average 6 links per agent. 3 are infected initially.
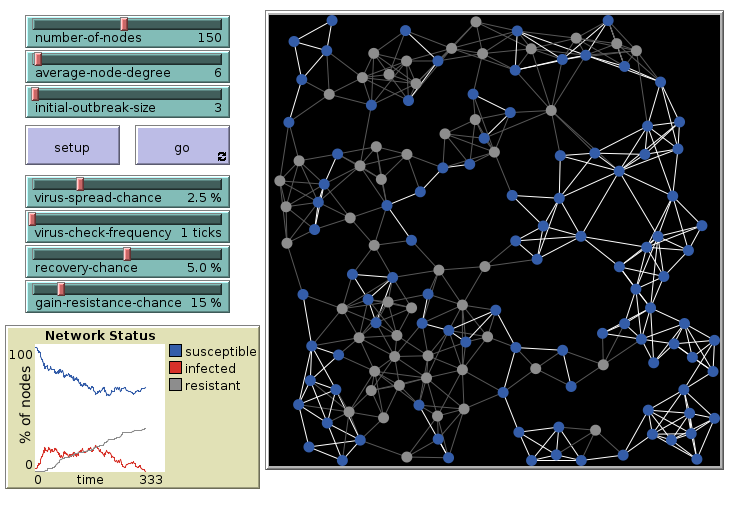
Virus on a Network: 6 links, final
The outbreak dies out after some time.
Virus on a Network: 15 links, initial
Repeat the simulation with 15 links per agent. 3 are infected initially. 
Virus on a Network: 15 links, final
The outbreak had infected most agents.
SI model
Now, we only treat the SI part of the model. We ignore recovery.
- People who are susceptible can become infected through contact with infectious
- People who are infectious stay infectious
The parameter \(\beta\) is the average number of contacts per unit time multiplied with the probability that an infection happens during such a contact.
SI-model: Simulation in R
- We produce a vector of length \(N\) with entries representing the state of each individual as
"S"or"I". - We model the random infection process in each step of unit time
Setup
Parameters: \(N=150, \beta=0.3\), a function to produce randomly infect individuals
[1] TRUE TRUE FALSE TRUE TRUE TRUESI-model: Simulation in R
Iteration over 75 time steps.
tmax <- 75
sim_run <- list(init) # list with one element
# This list will collect the states of
# all individuals over tmax time steps
for (i in 2:tmax) {
# Every agents has a contact with a random other
contacts <- sample(sim_run[[i-1]], size = N)
sim_run[[i]] <- if_else( # vectorised ifelse
# conditions vector: contact is infected
# and a random infection happens
contacts == "I" & randomly_infect(N, beta),
true = "I",
false = sim_run[[i-1]]
) # otherwise state stays the same
}
sim_output <- tibble( # create tibble for ggplot
# Compute a vector with length tmax
# with the count of "I" in sim_run list
t = 0:(tmax-1), # times steps
# count of infected, notice map_dbl
infected = map_dbl(sim_run, \(x) sum(x == "I")))
sim_output |>
ggplot(aes(t,infected)) + geom_line() +
theme_minimal(base_size = 20)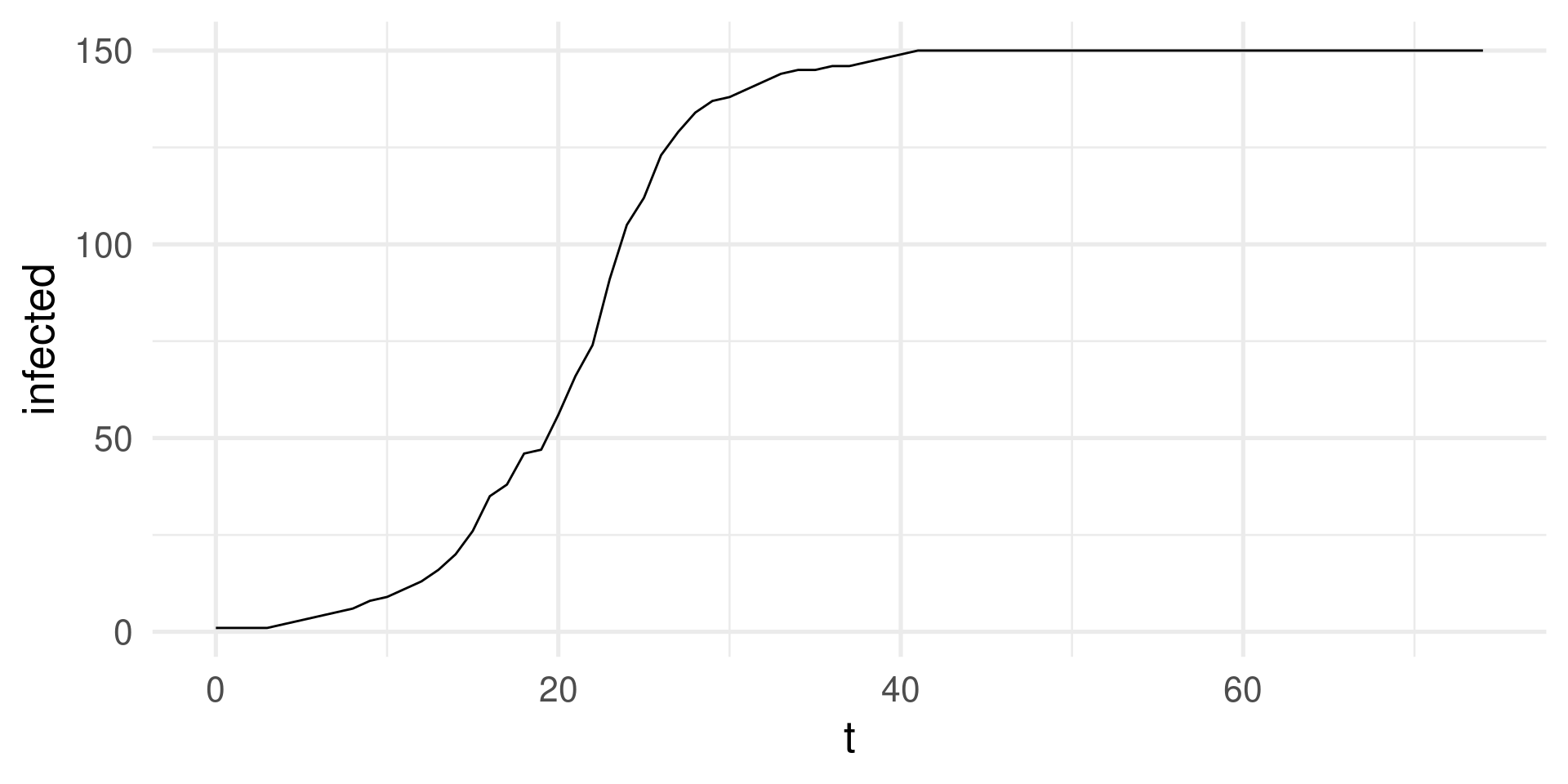
SI-model: Simulation in R
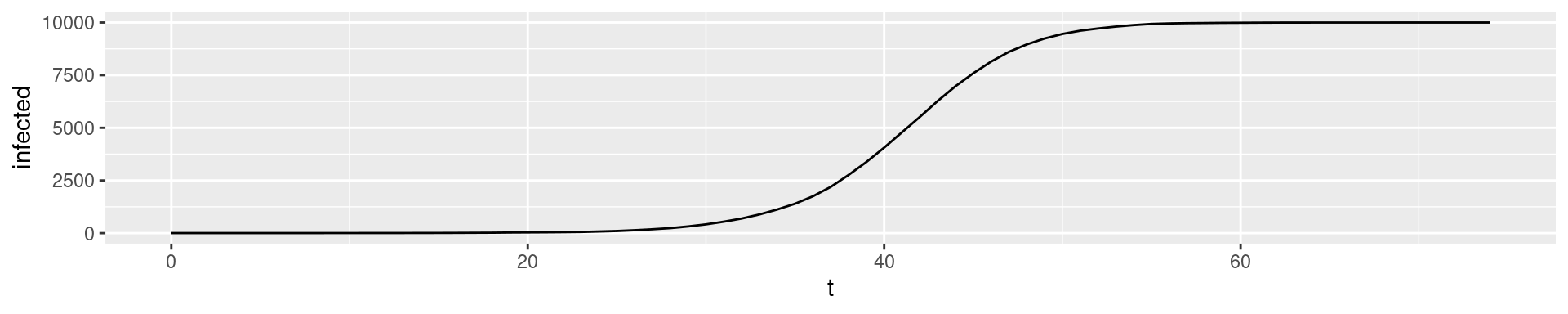
Run with \(N = 10000\)
N <- 10000
init <- rep("S",N) # All susceptible
init[1] <- "I" # Infect one individual
tmax <- 75
sim_run <- list(init) # list with one element
# This list will collect the states of
# all individuals over tmax time steps
for (i in 2:tmax) {
# Every agents has a contact with a random other
contacts <- sample(sim_run[[i-1]], size = N)
sim_run[[i]] <- if_else( # vectorised ifelse
# conditions vector: contact is infected
# and a random infection happens
contacts == "I" & randomly_infect(N, beta),
true = "I",
false = sim_run[[i-1]]
) # otherwise state stays the same
}
sim_output <- tibble( # create tibble for ggplot
# Compute a vector with length tmax
# with the count of "I" in sim_run list
t = 0:(tmax-1), # times steps
# count of infected, notice map_dbl
infected = map_dbl(sim_run, \(x) sum(x == "I")))
sim_output |>
ggplot(aes(t,infected)) + geom_line() +
theme_minimal(base_size = 20)
New programming concepts
From base R:
runif random numbers from uniform distribution
sample random sampling from a vector
for loop over commands with index (i) taking values of a vector (2:tmax) one by one if_else vectorized version of conditional statements
Calculus
The mathematics of the change and the accumulation of quantities
Motivation: SI model with
population compartments
Two compartments:
\(S(t)\) is the number of susceptible people at time \(t\).
\(I(t)\) is the number of infected people at time \(t\).
It always holds \(S(t) + I(t) = N\). (The total population is constant.)
How many infections per time?
The change of the number of infectious
\[\frac{dI}{dt} = \underbrace{\beta}_\text{infection prob.} \cdot \underbrace{\frac{S}{N}}_\text{frac. of $S$ still there} \cdot \underbrace{\frac{I}{N}}_\text{frac. $I$ to meet} \cdot N = \frac{\beta\cdot S\cdot I}{N}\]
where \(dI\) is the change of \(I\) (the newly infected here) and \(dt\) the time interval.
Interpretation: The newly infected are from the fraction of susceptible times the probability that they meet an infected times the infection probability times the total number of individuals.
Same logic as our Simulation in R!
Using \(S = N - I\) we rewrite
\[\frac{dI}{dt} = \frac{\beta (N-I)I}{N}\]
Ordinary differential equation
We interpret \(I(t)\) as a function of time which gives us the number of infectious at each point in time. The change function is now
\[\frac{dI(t)}{dt} = \frac{\beta (N-I(t))I(t)}{N}\]
and \(\frac{dI(t)}{dt}\) is also called the derivative of \(I(t)\).
Derivatives
- The derivative of a function is also a function with the same domain.
- Measures the sensitivity to change of the function output when the input changes (a bit)
- Example from physics: The derivative of the position of a moving object is its speed. The derivative of its speed is its acceleration.
- Graphically: The derivative is the slope of a tangent line of the graph of a function.
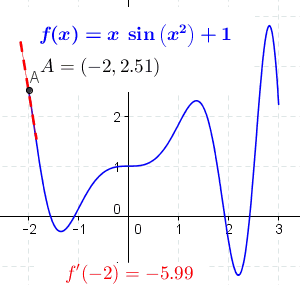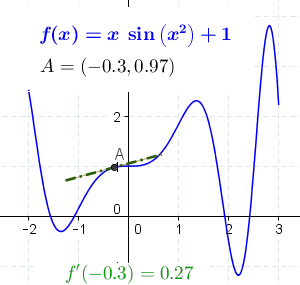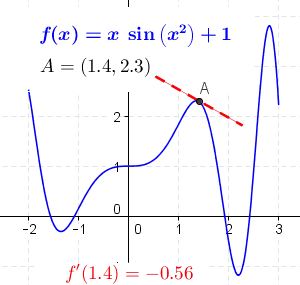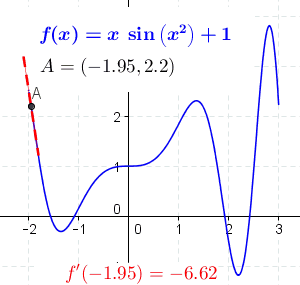
Differentiation
is the process to compute the derivative. For parameters \(a\) and \(b\) and other functions \(g\) and \(h\), rules of differentiation are
Function \(f(x)\)
Its derivative \(\frac{df(x)}{dx}\) or \(\frac{d}{dx}f(x)\) or \(f'(x)\)
\(a\cdot x\)
\(b\)
\(x^2,\ x^{-1} = \frac{1}{x},\ x^k\)
\(g(x) + h(x)\)
\(g(x)\cdot h(x)\)
\(g(h(x))\)
\(e^x,\ 10^x = e^{\log(10)x}\)
\(\log(x)\)
\(a\)
\(0\)
\(2\cdot x,\ -x^{-2} = -\frac{1}{x^2},\ k\cdot x^{k-1}\)
\(g'(x) + h'(x)\)
\(g'(x)\cdot h(x) + g(x)\cdot h'(x)\) (product rule)
\(g'(h(x))\cdot h'(x)\) (chain rule)
\(e^x,\ 10^x = \log(10)\cdot10^x\)
\(\frac{1}{x}\) (A surprising relation to me at least)
Differential equation
In a differential equation the unknown is a function!
We are looking for a function which derivative is a function of the function itself.
Example: SI-model
\[\frac{dI(t)}{dt} = \frac{\beta (N-I(t))I(t)}{N}\]
Which function \(I(t)\) fulfills this equation?
The analytical solution1
\(I(t) = \frac{N}{1 + (\frac{N}{I(0)} - 1)e^{-\beta t}}\)
Which is called the logistic equation. Note, we need to specify the initial number of infectious individuals \(I(0)\).
SI-model: Logistic Equation
\(I(t) = \frac{N}{1 + (\frac{N}{I(0)} - 1)e^{-\beta t}}\)
Plot the equation for \(N = 10000\), \(I_0 = 1\), and \(\beta = 0.3\)
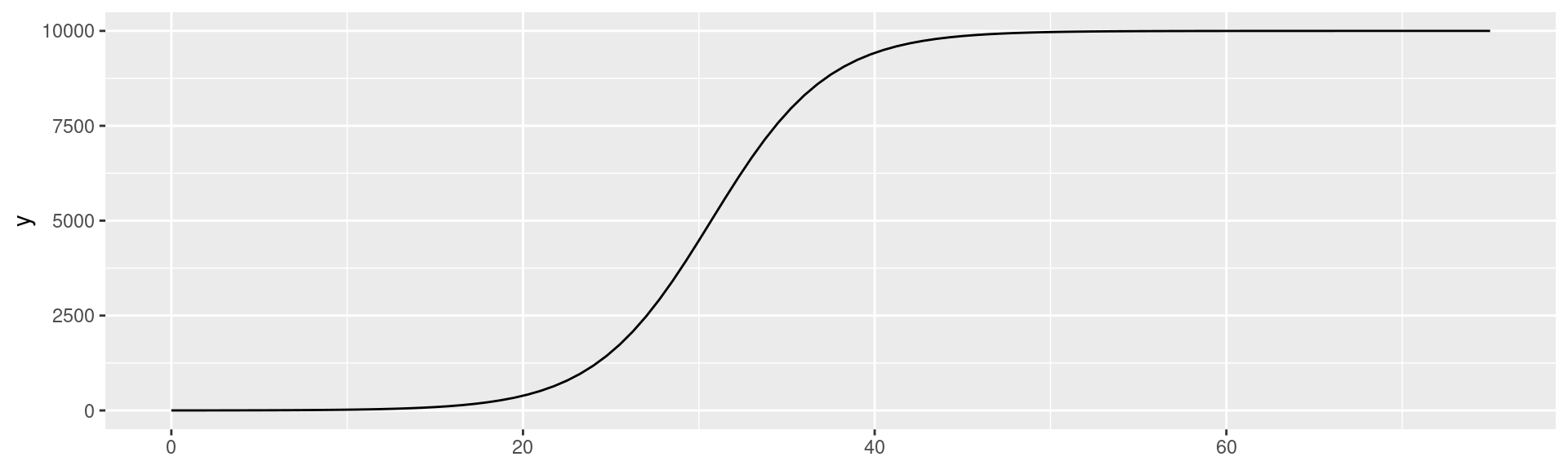
SI-model: Numerical integration
Another way of solution using, e.g., using Euler’s method.
We compute the solution step-by-step using increments of, e.g. \(dt = 1\).
N <- 10000
I0 <- 1
dI <- function(I,N,b) b*I*(N - I)/N
beta <- 0.3
dt <- 1 # time increment,
# supposed to be infinitesimally small
tmax <- 75
t <- seq(0,tmax,dt)
# this is the vector of timesteps
It <- I0 # this will become the vector
# of the number infected I(t) over time
for (i in 2:length(t)) {
# We iterate over the vector of time steps
# and incrementally compute It
It[i] = It[i-1] + dt * dI(It[i-1], N, beta)
# This is called Euler's method
}
tibble(t, It) |> ggplot(aes(t,It)) +
geom_function(
fun = function(t) N / (1 + (N/I0 - 1)*exp(-beta*t))) +
# Analytical solution for comparison
geom_line(color = "red") + # The numerical solution in black
theme_minimal(base_size = 20)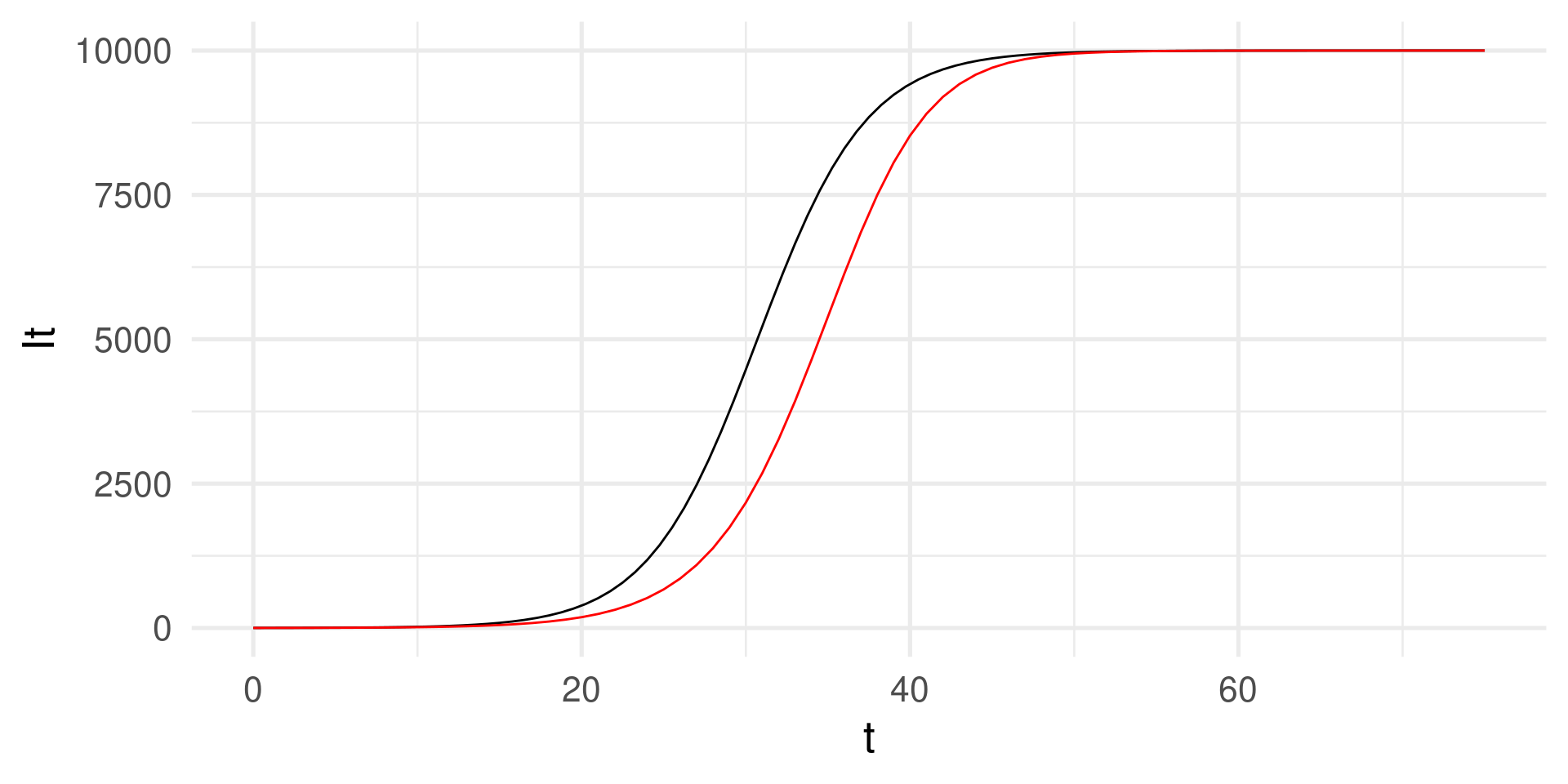
Why do the graphs deviate? The step size must be “infinitely” small
Numerical integration with smaller \(dt\)
We compute the solution step-by-step using small increments of, e.g. \(dt = 0.01\).
N <- 10000
I0 <- 1
dI <- function(I,N,b) b*I*(N - I)/N
beta <- 0.3
dt <- 0.01 # time increment,
# supposed to be infinitesimally small
tmax <- 75
t <- seq(0,tmax,dt)
# this is the vector of timesteps
It <- I0 # this will become the vector
# of the number infected I(t) over time
for (i in 2:length(t)) {
# We iterate over the vector of time steps
# and incrementally compute It
It[i] = It[i-1] + dt * dI(It[i-1], N, beta)
# This is called Euler's method
}
tibble(t, It) |> ggplot(aes(t,It)) +
geom_function(
fun = function(t) N / (1 + (N/I0 - 1)*exp(-beta*t))) +
# Analytical solution for comparison
geom_line(color = "red") + # The numerical solution in black
theme_minimal(base_size = 20)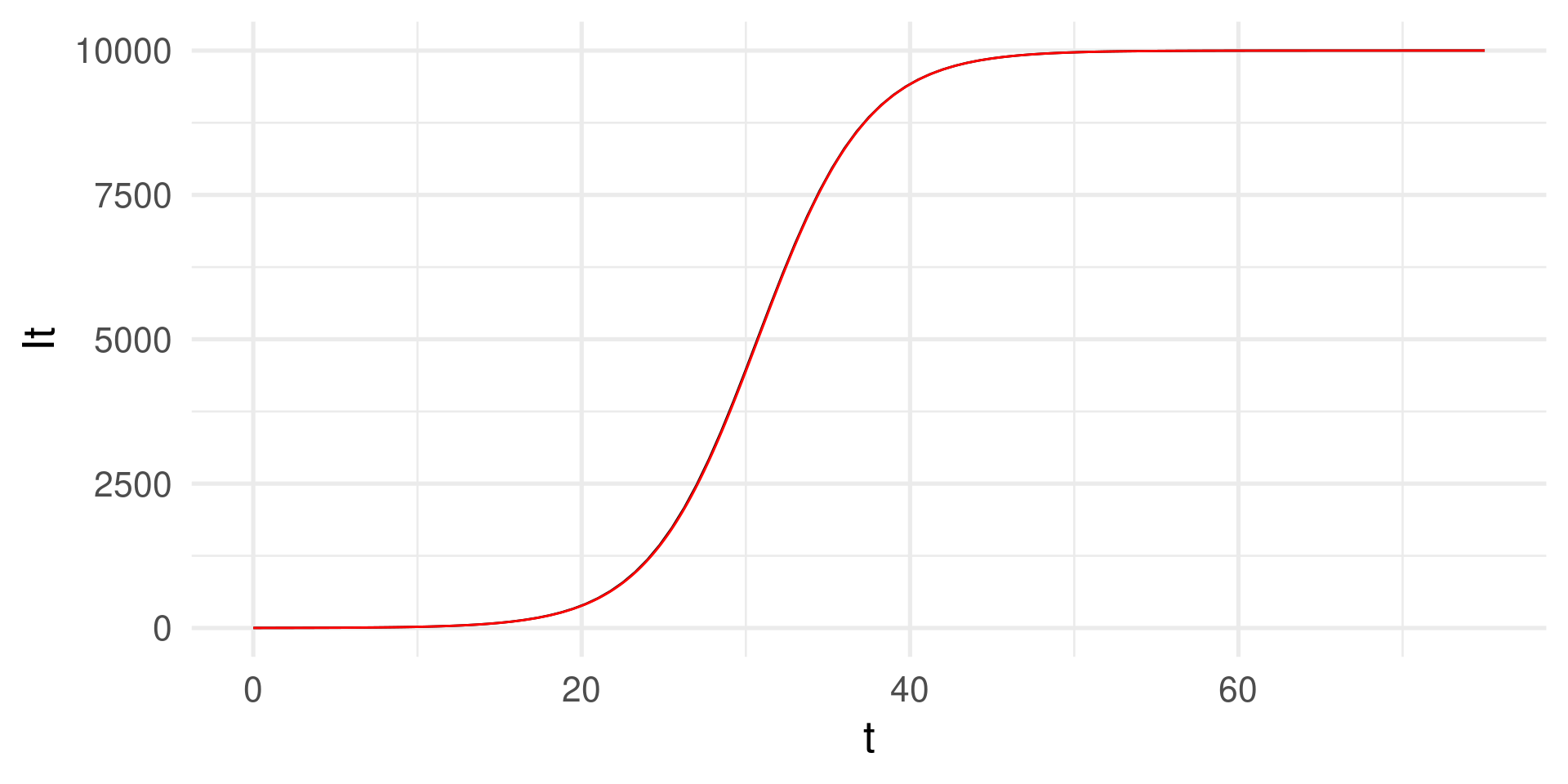
Mechanistic model
The SI model is a potential answer to the mechanistic question How do epidemics spread?
The examples above show 3 different ways to explore the model:
- Agent-based simulation
- We model every individual explicitly
- Simulation involve random numbers! So simulation runs can be different!
- Numerical integration of differential equation
- Needs a more abstract concept of compartments
- Analytical solutions of differential equation
- often not possible (therefore numerical integration is common)
Differentiation with data
We can do calculus operations with data!
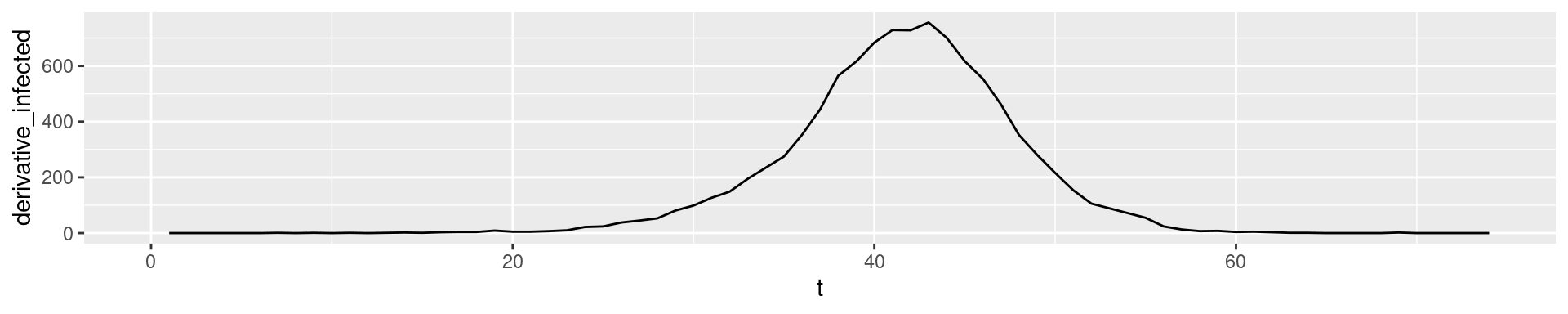
In empirical data we can compute the increase in a vector with the function diff:
The diff of our simulation output
2nd derivative: Change of change
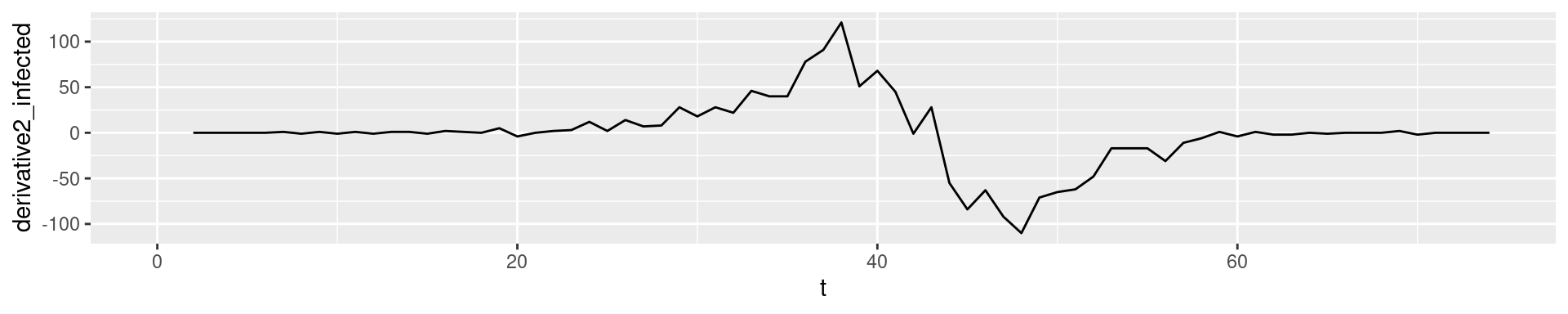
In empirical data: Derivatives of higher order tend to show fluctuation
Interpretation in SI-model

- \(I(t)\) total number of infected
- \(I'(t)\) number of new cases per day (time step)
- \(I''(t)\) how the number of new cases has changes compared to yesterday
- 2nd derivatives are a good early indicator for the end of a wave.
Integration
The integral of the daily new cases from the beginning to day \(s\) is \(\int_{-\infty}^s f(t)dt\) and represents the total cases at day \(s\).
- The integral of a function \(f\) up to time \(s\) is also called the anti-derivative \(F(s) = \int_{-\infty}^s f(t)dt\).
- The symbol \(\int\) comes from an S and means “sum”.
- Compute the anti-derivative of data vector with
cumsum.
- Empirically: Derivatives tend to become noisy, while integrals tend to become smooth.
The fundamental theorem of calculus
The integral of the derivative is the function itself.
This is not a proof but shows the idea:
[1] 1 3 7 12 17 20 20[1] 1 2 4 5 5 3 0[1] 1 2 1 0 -2 -3[1] 1 2 4 5 5 3 0Linear Model
The first work-horse to explore relations between numerical variables
Different purposes of models
Agent-based models and differential equations are usually used to explain the dynamics of one or more variables typically over time. They are used to answer mechanistic questions.
In the following we treat variable-based models which we use to
- explain relations between variables
- make predictions
These are often used to answer inferential and predictive questions.
(With experimental or more theoretical effort also for causal questions.)
First, we focus on linear models.
Hello again penguins!
We use the dataset Palmer Penguins
Chinstrap, Gentoo, and Adélie Penguins



# A tibble: 344 × 8
species island bill_length_mm bill_depth_mm flipper_length_mm body_mass_g
<fct> <fct> <dbl> <dbl> <int> <int>
1 Adelie Torgersen 39.1 18.7 181 3750
2 Adelie Torgersen 39.5 17.4 186 3800
3 Adelie Torgersen 40.3 18 195 3250
4 Adelie Torgersen NA NA NA NA
5 Adelie Torgersen 36.7 19.3 193 3450
6 Adelie Torgersen 39.3 20.6 190 3650
7 Adelie Torgersen 38.9 17.8 181 3625
8 Adelie Torgersen 39.2 19.6 195 4675
9 Adelie Torgersen 34.1 18.1 193 3475
10 Adelie Torgersen 42 20.2 190 4250
# ℹ 334 more rows
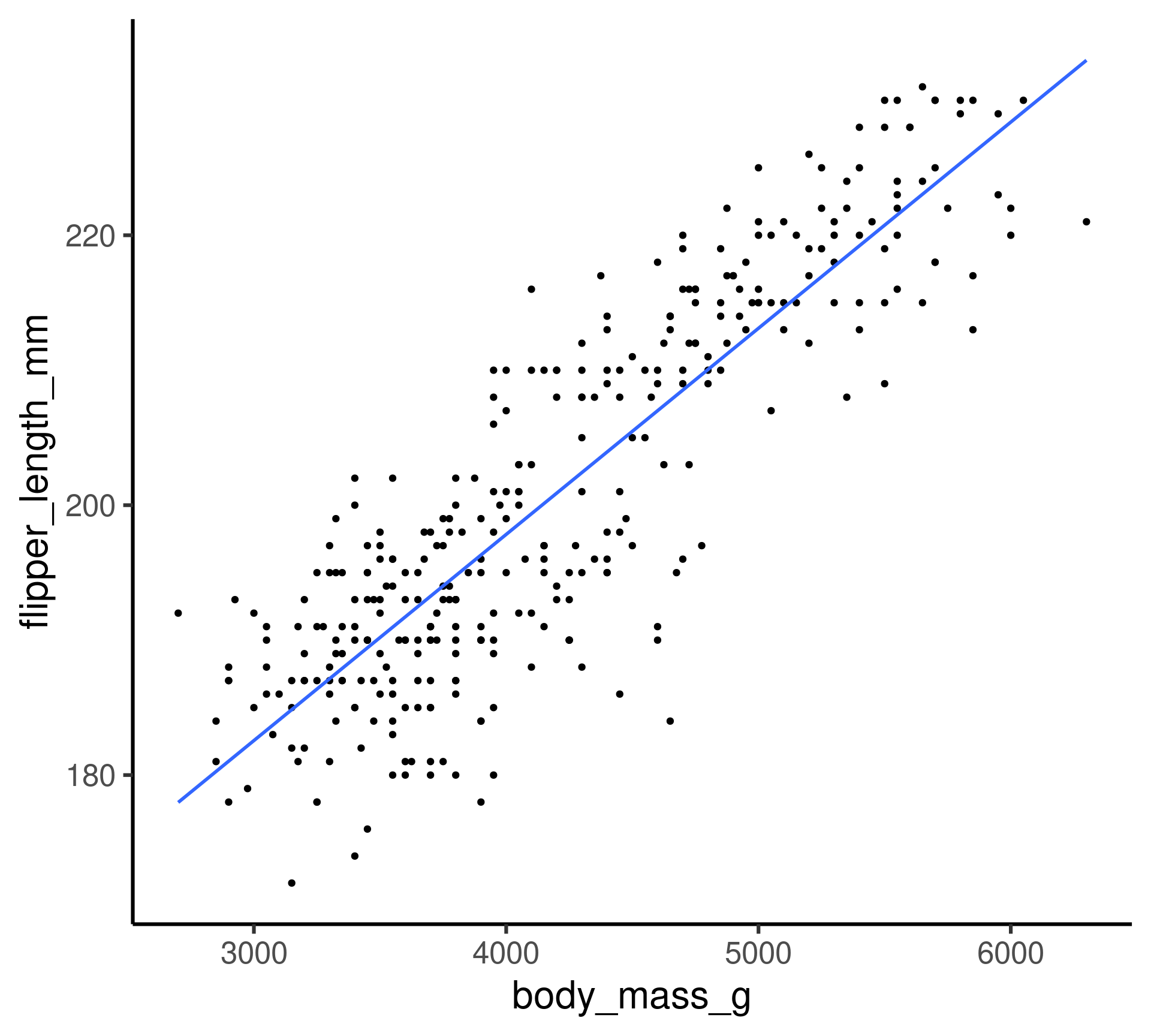
# ℹ 2 more variables: sex <fct>, year <int>Body mass in grams
Flipper length in millimeters
Relate variables as a line
A line is a shift-scale transformation of the identity function usually written in the form
\[f(x) = a\cdot x + b\]
where \(a\) is the slope, \(b\) is the intercept.1
a <- 0.5
b <- 1
func <- function(x) a*x + b
ggplot() + geom_function(fun = func, size = 2) +
# Set axis limits and make axis equal
xlim(c(-0.5,2)) + ylim(c(0,2)) + coord_fixed() +
geom_line( # intercept line:
data=tibble(x=c(0,0),y=c(0,1)),
mapping = aes(x,y),
color = "blue", size = 2) +
geom_line( # slope:
data=tibble(x=c(1.5,1.5),y=c(1.25,1.75)),
mapping = aes(x,y),
color = "red", size = 2) +
geom_line( # x-interval of length one:
data=tibble(x=c(0.5,1.5),y=c(1.25,1.25)),
mapping = aes(x,y), color = "gray") +
theme_classic(base_size = 24)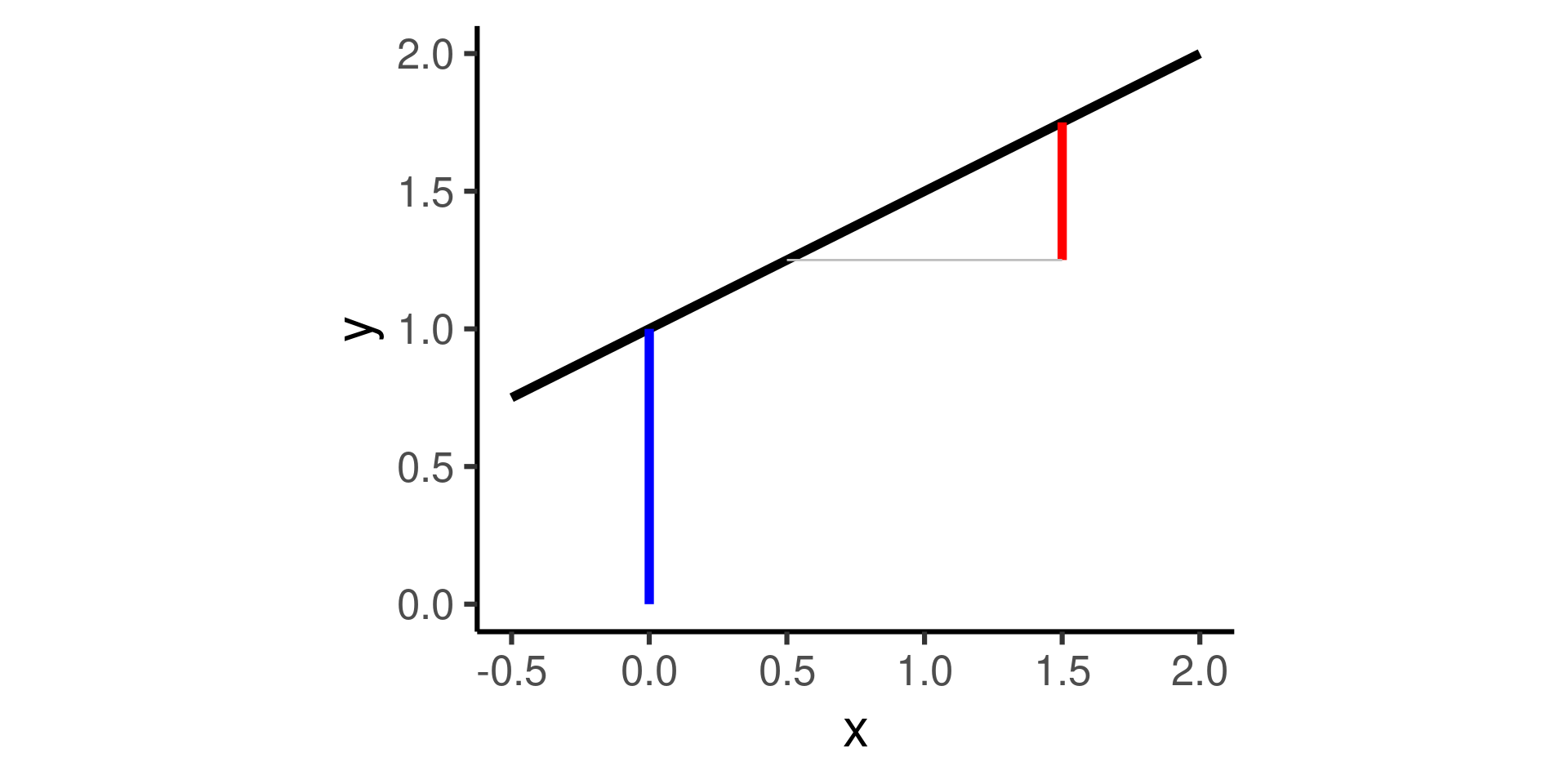
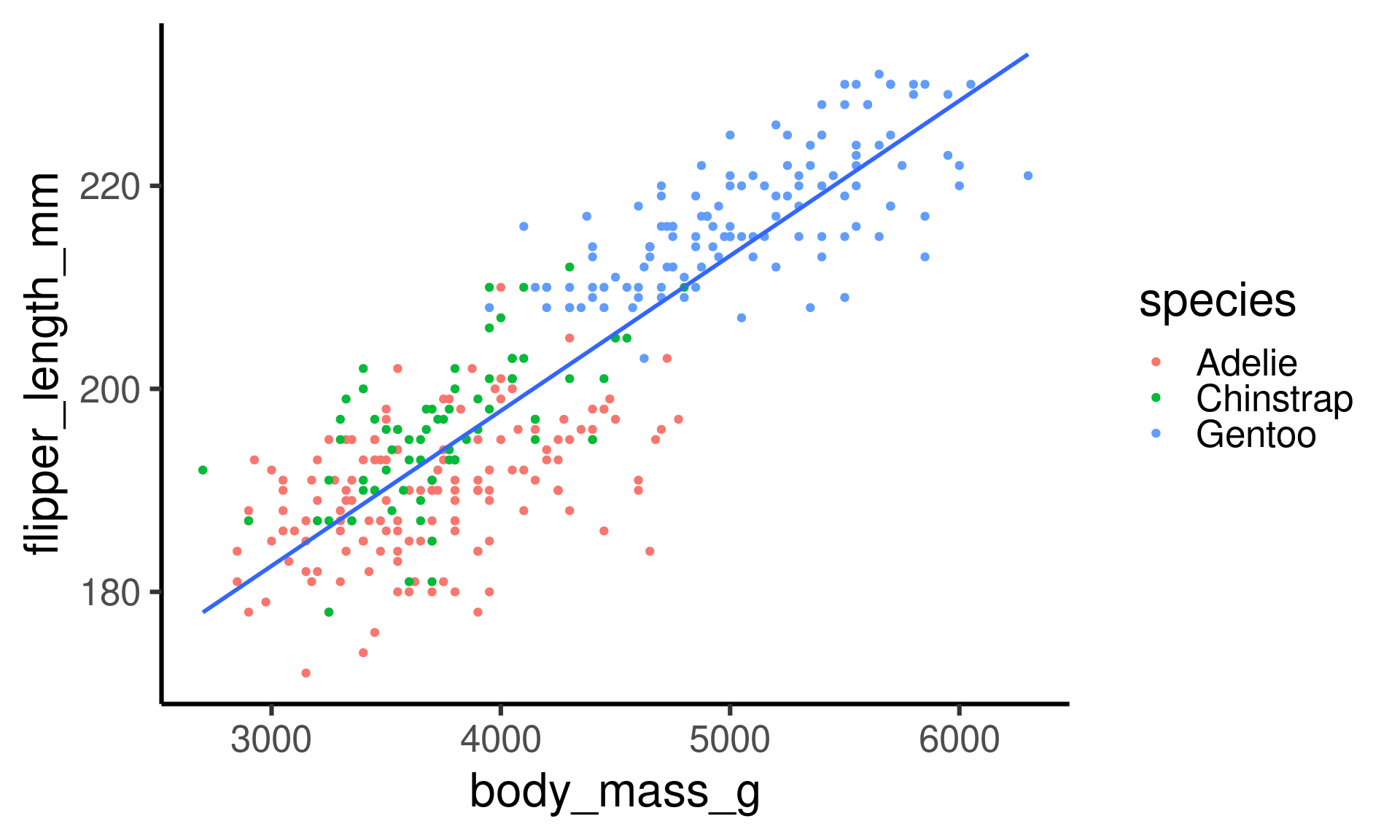
Penguins: Linear model
Flipper length as a function of body mass.
Penguins: A smooth line
Flipper length as a function of body mass with loess1 smoothing.
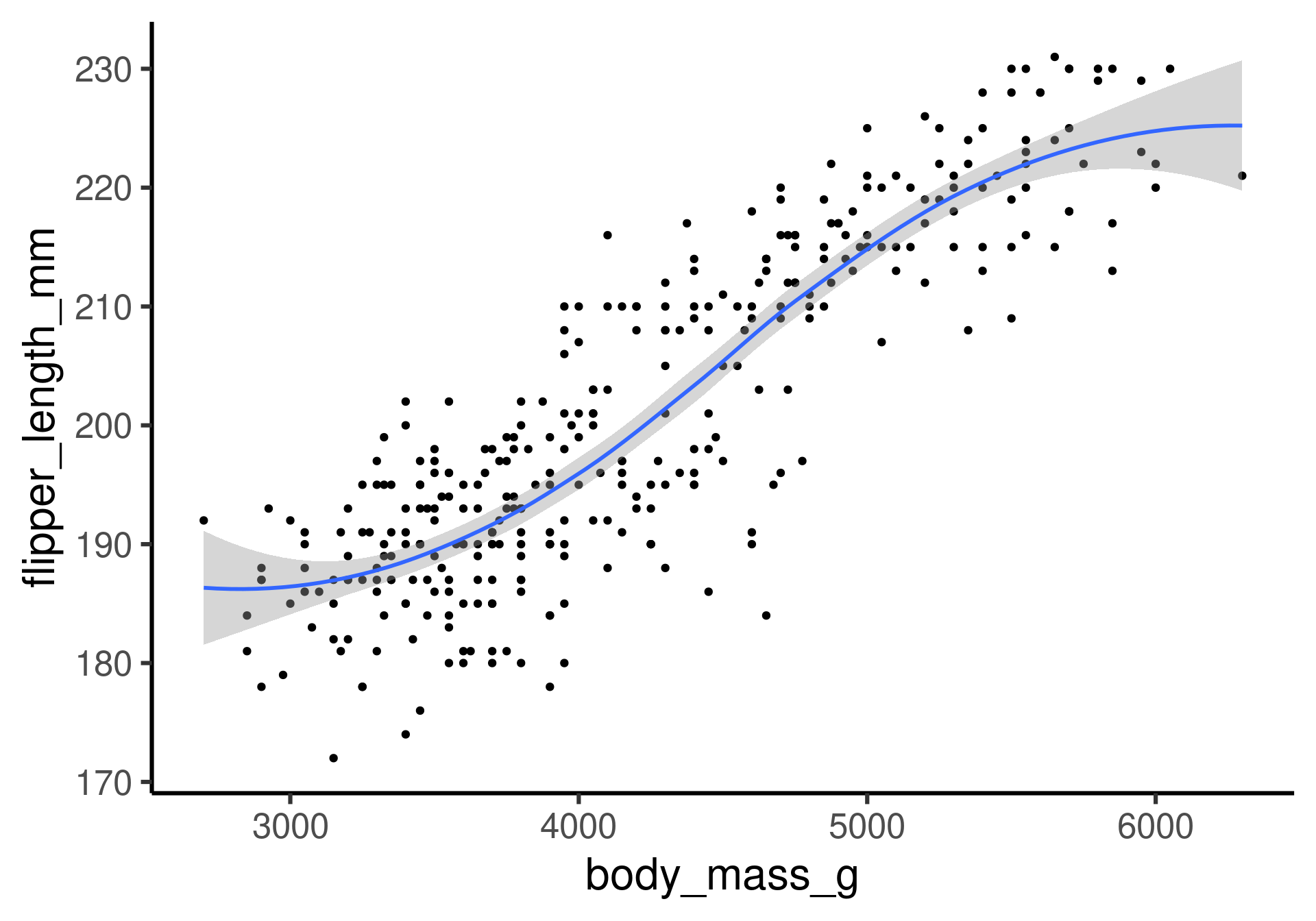
This is a less theory-driven and more data-driven model. Why?
We don’t have a simple mathematical form of the function.
Terminology variable-based models
- Response variable:1 Variable whose behavior or variation you are trying to understand, on the y-axis
- Explanatory variable(s):2 Other variable(s) that you want to use to explain the variation in the response, on the x-axis
- Predicted value: Output of the model function.
- The model function gives the (expected) average value of the response variable conditioning on the explanatory variables
- Residual(s): A measure of how far away a case is from its predicted value (based on the particular model)
Residual = Observed value - Predicted value
The residual tells how far above/below the expected value each case is
More explanatory variables
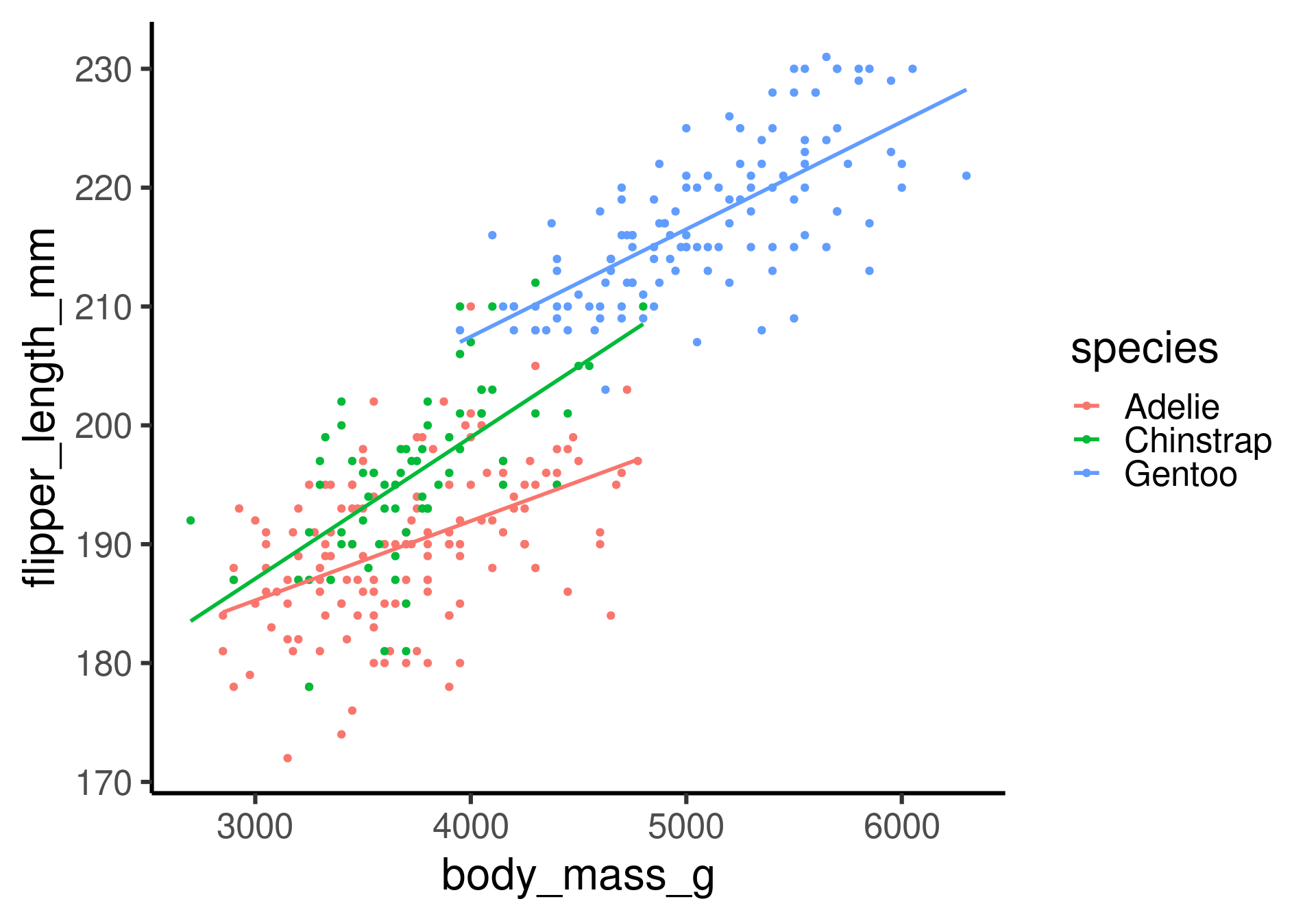
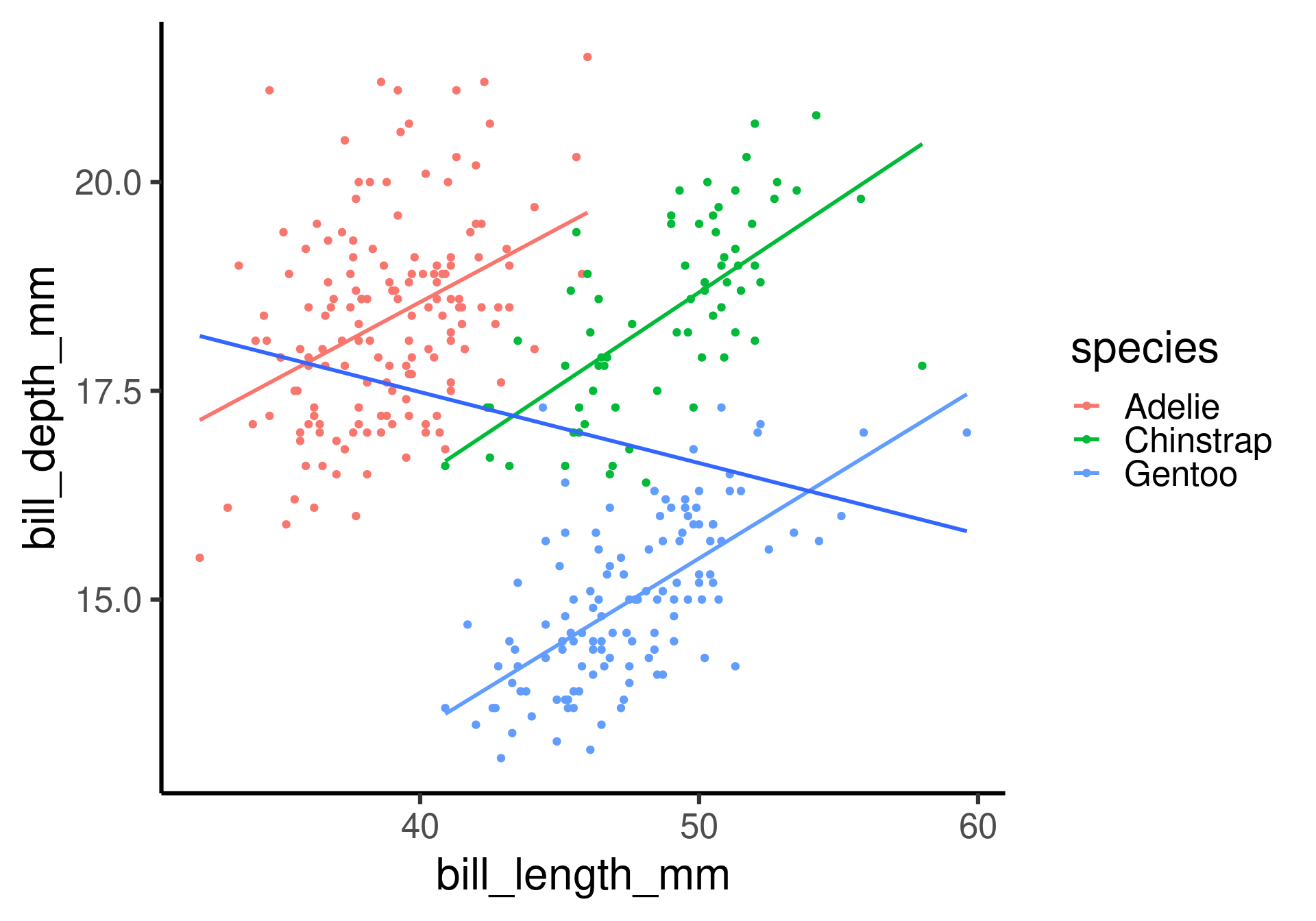
How does the relation between flipper length and body mass change with different species?
ggplot-hint: How to color penguins but keep one model?
Put the mapping of the color aesthetic into the geom_point command.
Beware of Simpson’s paradox
Slopes for all groups can be in the opposite direction of the main effect’s slope!
 ::: aside Source: https://upload.wikimedia.org/wikipedia/commons/f/fb/Simpsons_paradox_-_animation.gif :::
::: aside Source: https://upload.wikimedia.org/wikipedia/commons/f/fb/Simpsons_paradox_-_animation.gif :::
The paradox is real!
How does the relation between bill length and body mass change with different species?
Models - upsides and downsides
- Models can reveal patterns that are not evident in a graph of the data. This is an advantage of modeling over simple visual inspection of data.
- How would you visualize dependencies of more than two variables?
- The risk is that a model is imposing structure that is not really there in the real world data.
- People imagined animal shapes in the stars. This is maybe a good model to detect and memorize shapes, but it has nothing to do with these animals.
- Every model is a simplification of the real world, but there are good and bad models (for particular purposes).
- A skeptical (but constructive) approach to a model is always advisable.
Variation around a model
… is as interesting and important as the model!
Statistics is the explanation of uncertainty of variation in the context of what remains unexplained.
- The scattered data of flipper length and body mass suggests that there maybe other factors that account for some parts of the variability.
- Or is it randomness?
- Adding more explanatory variables can help (but need not)
All models are wrong …
… but some are useful. (George Box)
Extending the range of the model:
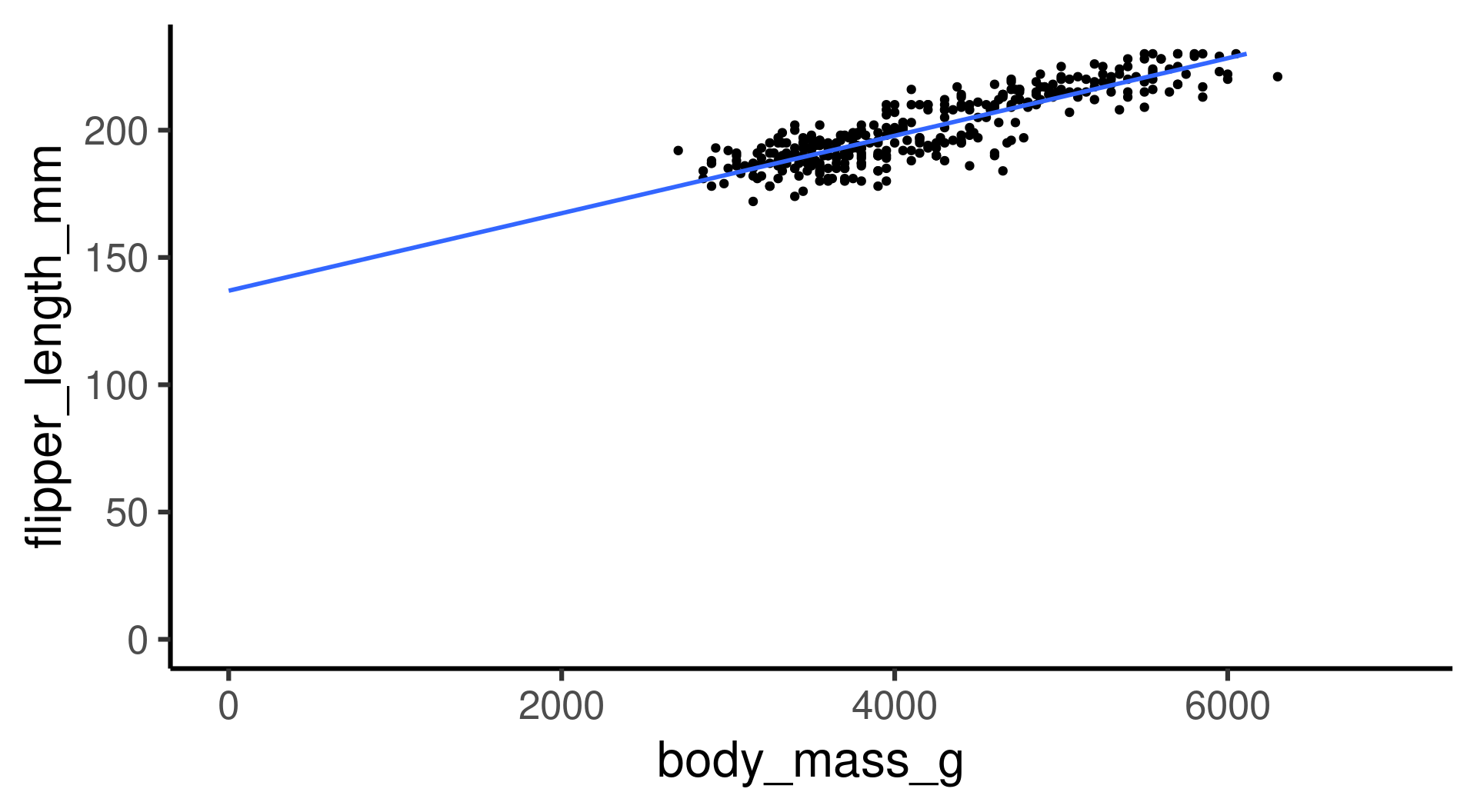
- The model predicts that penguins with zero weight still have flippers of about 140 mm on average.
- Is the model useless? Yes, around zero body mass. No, it works OK in the range of the body mass data.
Two model purposes
Linear models can be used for:
- Explanation: Understand the relationship of variables in a quantitative way.
For the linear model, interpret slope and intercept. - Prediction: Plug in new values for the explanatory variable(s) and receive the expected response value.
For the linear model, predict the flipper length of new penguins by their body mass.
Fitting Models (Part 1)
Today: The linear model.
In R: tidymodels

Our goal
Predict flipper length from body mass
average flipper_length_mm \(= \beta_0 + \beta_1\cdot\) body_mass_g
Step 1: Specify model
Step 2: Set the model fitting engine
Step 3: Fit model and estimate parameters
Only now, the data and the variable selection comes in.
Use of formula syntax
parsnip model object
Call:
stats::lm(formula = flipper_length_mm ~ body_mass_g, data = data)
Coefficients:
(Intercept) body_mass_g
136.72956 0.01528 parsnip is package in tidymodels which is to provide a tidy, unified interface to models that can be used to try a range of models.
What does the output say?
parsnip model object
Call:
stats::lm(formula = flipper_length_mm ~ body_mass_g, data = data)
Coefficients:
(Intercept) body_mass_g
136.72956 0.01528 average flipper_length_mm \(= 136.72956 + 0.01528\cdot\) body_mass_g
Interpretation:
The penguins have a flipper length of 138 mm plus 0.01528 mm for each gram of body mass (that is 15.28 mm per kg). Penguins with zero mass have a flipper length of 138 mm. However, this is not in the range where the model was fitted.
Show output in tidy form
Parameter estimation
Notation from statistics: \(\beta\)’s for the population parameters and \(\hat\beta\)’s for the parameters estimated from the sample statistics.
\[\hat y = \beta_0 + \beta_1 x\]
Is what we cannot have. (\(\hat y\) stands for predicted value of \(y\). )
We estimate \(\hat\beta_0\) and \(\hat\beta_1\) in the model fitting process.
\[\hat y = \hat\beta_0 + \hat\beta_1 x\]
A typical follow-up data analysis question is what the fitted values \(\hat\beta_0\) and \(\hat\beta_1\) tell us about the population-wide values \(\beta_0\) and \(\beta_1\)?
This is the typical inferential question.
Fitting Linear Models Part 2
Next week!